- 等差数列的性质及应用
- 共275题
已知数列






17.求数列
18.设



正确答案
详见解析
解析
(Ⅰ)设数列


由
解得
故数列

考查方向
等差数列的通项公式
解题思路
根据题意建立首项和公差的等量关系,然后求解方程求出首项和公差,然后求出通项公式
易错点
数列通项公式记忆错误
正确答案
详见解析
解析
(Ⅱ)由(1)可得
所以当

①-②得

又




考查方向
数列求和
解题思路
利用裂项相消的方法求数列的和
易错点
计算能力弱,公式定理记忆混淆
对未取得基金代销业务资格、擅自开办基金销售业务的机构及其负责人,( )。
A.责令机构关闭
B.追究刑事责任
C.对相关负责人革职
D.责令改正,并处以警告、罚款
正确答案
D
解析
[解析] 未取得基金代销业务资格,擅自开办基金销售业务的,责令改正,并处以警告、罚款;对直接负责的主管人员和其他直接责任人员,处以警告、罚款。
16.设等差数列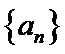
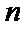
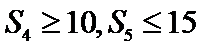
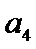
正确答案
4
解析
∵等差数列{an}的前n项和为Sn,且S4≥10,S5≤15
∴ S4=4a1+(4×3)/2d≥10
S5=5a1+(5×4)/2d≤15
即 2a1+3d≥5
a1+2d≤3
∴ a4=a1+3d≥(5-3d)/2 +3d≥(5+3d)/2
a4=a1+3d=(a1+2d)+d≤3+d
∴(5+3d)2 ≤a4≤3+d,5+3d≤6+2d,d≤1
∴a4≤3+d≤3+1=4故a4的最大值为4,
考查方向
等差数列的前n项和;等差数列.
解题思路
利用等差数列的前n项和公式变形为不等式,再利用消元思想确定d或a1的范围,a4用d或a1表示,再用不等式的性质求得其范围
易错点
注意等差数列公式的变形,确定其范围。
教师点评
此题重点考查等差数列的通项公式,前n项和公式,以及不等式的变形求范围;
知识点
已知各项均不为0的等差数列







17.求数列

18.设



正确答案
则

解析
则

考查方向
求数列的通项公式
解题思路
根据已知条件建立方程关系,通过求解基本量求数列通项。
易错点
注意数列类别的判定,能够根据数列的等量关系正确运算基本量
教师点评
正确列出等量关系,能够准确运算基本量是解题关键
正确答案

则
解析

则
考查方向
错位相减求和
解题思路
先根据通项写出数列,然后应用错位相减法求和
易错点
(1)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.(2)公比q为参数时要分q=1和q≠1讨论.
教师点评
注意表达式的“错项对齐”,错位后共有n+1项,∴中间n-1项是等比数列求和.
13.中位数1010的一组数构成等差数列,其末项为2015,则该数列的首项为( )
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)证明:
(2)是否存在

(3)是否存在


正确答案
(1)证明:因为



所以



(2)令











假设存在





则

令




化简得






显然
因此不存在





(3)假设存在







则

分别在两个等式的两边同除以




则

将上述两个等式两边取对数,得
且
化简得
且
再将这两式相除,化简得

令
则
令
则
令

令

由

知





故



所以不存在







解析
解析已在路上飞奔,马上就到!
知识点
21.设








(1)证明:函数



(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为


正确答案
(1)
所以


又

所以


因为




(2)解法一:由题设,
设
当
当
若
若
所以


所以

综上所述,当


解法二 由题设,
当
当

当


假设

那么,当

又
令
所以当



当



所以
故

所以,对于一切

解法三:由已知,记等差数列为




所以
令
当


当
而


若


当


从而




所以当


综上所述,当


解析
解析已在路上飞奔,马上就到!
知识点
11. 已知数列






正确答案
解析














考查方向
解题思路
利用求和公式可得



易错点
①计算能力②递减数列的应用③注意恒成立问题。
知识点
扫码查看完整答案与解析



























