- 直线、平面垂直的判定与性质
- 共445题
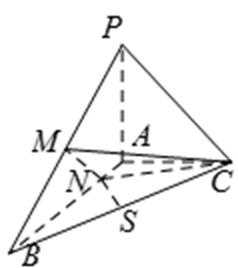
18.已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列命题:
① 已知
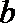
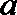
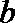
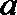

② 在二面角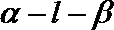
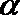
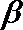
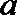
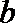
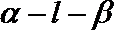
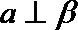
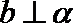
③已知异面直线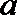
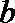
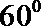
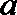
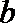
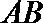
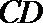
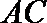
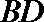
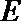
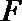
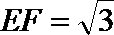
④若正三棱锥的内切球的半径为1,则此正三棱锥的体积最小值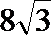
则正确命题的编号是
正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
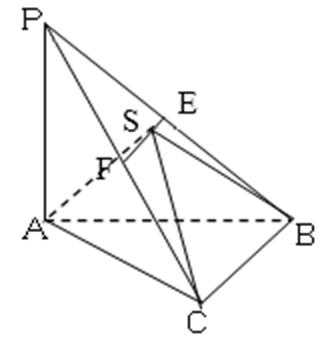
17.三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若
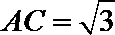
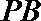
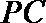
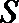

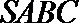
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 如图,已知长方体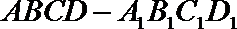
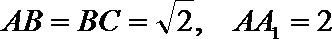

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,四边形ABCD是矩形,

(1)求证:AE
(2)求证:AE//平面BFD;
(3)求三棱锥C-BGF的体积。
正确答案
(1)∵ 
∴ 
∵ BF

又
∴ AE
(2) 依题意,易知G为AC的中点
又∵ BF

∴ 可知F为CE的中点
故可知 GF//AE
又可知
∴ AE//平面BFD
(3)由(1)可知AE
∴ GF
又 

∴
∴ 三棱锥C-BGF的体积为
解析
解析已在路上飞奔,马上就到!
知识点
20.在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求多面体ABCDE的体积;
(3)求直线EC与平面ABED所成角的正弦值。
正确答案
(1)
如图,由已知AB⊥平面ACD,DE⊥平面ACD,
∴AB//ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则

∴四边形ABFH是平行四边形,
∴
由


(2)取AD中点G,连接CG.
AB
∴CG
又CG
∴CG
∴



(3)连接EG,由(2)有CG
∴
设为

有
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱锥P﹣ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
(Ⅰ) 证明:EF∥平面PAB;
(Ⅱ) 求直线AC与平面ABEF所成角的正弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在直三棱柱

(1)证明:
(2)求直线

(3)求点A到平面
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
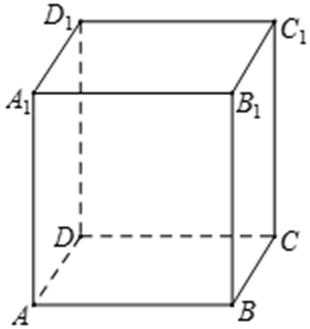
17.如图,在四棱柱ABCD﹣A1B1C1D1中,AB=BC=CA=
(Ⅰ)求证:BD⊥AA1;
(Ⅱ)求证:A1E∥平面DCC1D1
(Ⅲ) 若AA1⊥AC,求A1E与面ACC1A1所成角大小.
正确答案
(Ⅰ)证明:在四棱锥ABCD﹣A1B1C1D1中,
∵AB=BC=CA,且AD=DC,
取AC中点O,则BO⊥AC,DO⊥AC,∴B,O,D三点在一条直线上.
又∵面AA1C1C⊥面ABCD,面AA1C1C∩面ABCD=AC,BD⊂面ABCD,BD⊥AC,
∴BD⊥面AA1C1C,AA1⊂面AA1C1C,∴BD⊥AA1;
(Ⅱ)证明:连AE,在Rt△DCO中∠DCO=30°
在正△BCA中,∠BCO=60°,∴DC⊥BC,
又在正△BCA中,AE⊥BC,
∴AE∥DC,
又AE⊄面DCC1D1,DC⊂面DCC1D1,∴AE∥面DCC1D1,
在四棱锥中,AA1∥DD1,AA1⊄面DCC1D1,DD1⊂面DCC1D1,
∴AA1∥面DCC1D1,
又AA1∩AE=A,
∴面A1AE∥面DCC1D1,
又A1E⊂面AA1E,故A1E∥面DCC1D1.
(Ⅲ)解:过E作AC的垂线,设垂足为N,∵面ABCD⊥面AA1C1C,∴EN⊥面AA1C1C,
连A1N,则A1N为A1E在面AA1C1C内的射影,
∴∠EA1N为直线A1E与面AC1所成角,
由已知得:

解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱柱










(1)证明:
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析