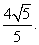- 空间直角坐标系
- 共20题
10.如下图,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.四棱锥ABCD中,E、H分别是AB、AD的中点,F、G分别是CB、CD的中点,若AC+BD=3,AC·BD=1,则EG2+FH2=________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
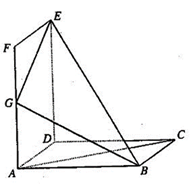
如图所示,正方形ABCD和矩形ADEF所在平面相互垂直,G是AF的中点。

(2)若直线BE与平面ABCD成45o角,求平面GBE
正确答案

解析
证明:
连结BD交AC于点M,取BE的中点N,
连结MN,则MN∥ED且MN=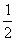
知AG∥ED且AG=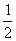
∴MN∥AG且MN=AG。
故四边形MNAG是平行四边形,
AM∥GN,即AC∥GN,
又∵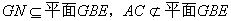
∴ AC∥平面GBE。
(2)
延长EG交DA的延长线于H点,
连结BH,作AP⊥BH于P点,连结GP。
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,
GH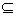
∴ GA⊥平面ABCD,由三垂线定理,知GP⊥BH,
故∠GPA就是所求二面角的平面角。
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD。
∴ ED⊥平面ABCD,
故∠EBD就是直线BE与平面ABCD成的角,
知∠EBD=45°,设AB=a,则BE=BD=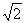
在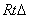
BH=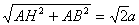
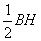
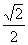
在
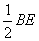
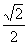
=AP ,GA⊥AP,知∠GPA=45°。
故平面GBE与平面ABCD所成的锐二面角的大小为45°。
知识点
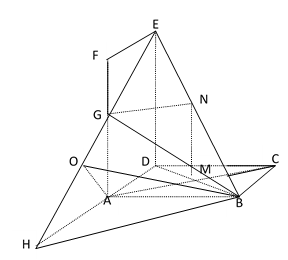
如图,在多面体





(1)求证:面

(2)求证:

正确答案
见解析。
解析
(1)








又




(2)
取

















又















知识点
若


正确答案
解析
因为







知识点
△ABC的外接圆的圆心为O,半径为1,



正确答案
解析
由







知识点
已知


正确答案
解析
略
知识点
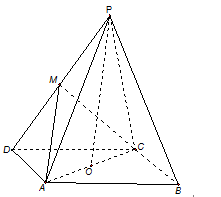
如图,在四棱锥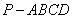
平行四边形,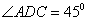
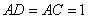
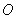
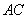
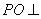
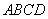
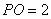
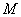
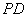
(1)证明: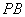
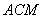
(2)证明: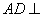
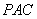
(3)求直线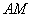
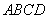
正确答案
见解析。
解析
(1)证明:连接BD,MO,在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点,又M为PD的中点,所以PB//MO。因为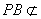
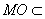
(2)证明:因为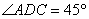
所以
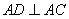
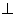
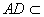
所以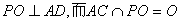
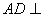
(3)解:取DO中点N,连接MN,AN,因为M为PD的中点,
所以MN//PO,且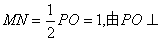
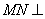
所以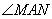
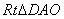
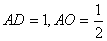
所以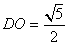
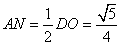
在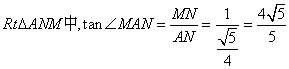
即直线AM与平面ABCD所成角的正切值为
知识点
在如图所示的空间直角坐标系O﹣xyz中,一个四面体的顶点坐标分别为(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出的编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )
正确答案
解析
在坐标系中,标出已知的四个点,根据三视图的画图规则,可得三棱锥的正视图和俯视图分别为④②
知识点
三棱柱ABC - A1B1C1各顶点都在一个球面上,侧棱与底面垂直,∠ACB = 120°,CA = CB =

正确答案
64π
解析
略
知识点
扫码查看完整答案与解析