- 空间几何体的结构特征
- 共715题
一简单组合体的三视图如图(2)所示,则该组合体的
体积为
正确答案
解析
由三视图知,此组合体为一个长为4,宽为3,高为1的长方体、中心去除一个半径为1的圆柱,故其体积为
知识点
某四棱锥的三视图如图所示,则最长的一条侧棱长度为( )
正确答案
解析
略
知识点
已知几何体由正方体和直三棱柱组成,其三视图和直观图(单位:cm)如图所示.设两条异面直线




正确答案
解析
(解释性理解水平、探究性理解水平/几何体的三视图,余弦定理,异面直线所成角)由


故


由题设知

取




由余弦定理,得
知识点
四棱锥
则四棱锥
正确答案
解析
略
知识点
已知某几何体的三视图,根据图中标出的尺寸 (单位:
正确答案
解析
由三视图可知,该几何体为底面是正方形,且边长为2cm,高为2cm的四棱锥,
如图,
故
故选B。
知识点
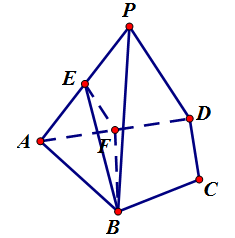
如图,在四棱锥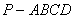
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD
正确答案
见解析
解析
证明:(1)在△PAD中,因为E、F分别为
AP,AD的中点,所以EF//PD.
又因为EF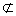
所以直线EF//平面PCD.
(2)连结DB,因为AB=AD,∠BAD=60°,
所以△ABD为正三角形,因为F是AD的
中点,所以BF⊥AD.因为平面PAD⊥平面
ABCD,BF
知识点
某几何体的三视图如图所示,则该几何体的体积为( )。
正确答案
解析
该几何体为一个半圆柱与一个长方体组成的一个组合体。
V半圆柱=
V长方体=4×2×2=16.
所以所求体积为16+8π.故选A.
知识点
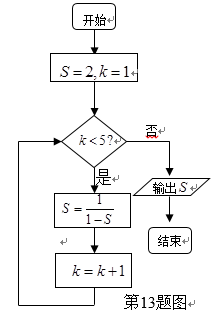
执行如右图的程序框图,那么输出
正确答案
-1
解析
第1次循环,S=﹣1,K=2,
第2次循环,S=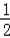
第3次循环,S=2,K=4,
第4次循环,S=﹣1,K=5,
…
框图的作用是求周期为3的数列,输出S的值,
不满足k<5,退出循环,循环次数是4次,即输出的结果为﹣1,
故答案为:﹣1。
知识点
一个几何体的三视图如右图所示,则该几何体的表面积为 ;
正确答案
2π+24
解析
略。
知识点
已知一棱锥的三视图如图2所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为
正确答案
解析
该几何体是底面为直角梯形的四棱锥,依题意得
知识点
扫码查看完整答案与解析