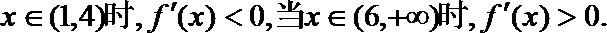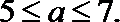- 球面距离及相关计算
- 共8题
11.在半径为1的球面上有不共面的四个点A,B,C,D且



正确答案
解析
构造一个长方体,使得四面体ABCD的六条棱分别是长方体某个面的对角线(如图).设长方体的长、宽、高分别为


考查方向
解题思路
构造法来解。
易错点
缺乏空间想象力。
知识点
16. 




正确答案
32
解析
如下图所示:


考查方向
解题思路
先求出球的半径再计算其表面积。
易错点
不会计算球的半径。
知识点
11.已知球








正确答案
解析
设球O的半径为r,球心O在平面ABC上的射影为M,则M为三角形ABC的外心,由





考查方向
解题思路
先确定M为三角形ABC外接圆的圆心;利用平面几何的知识求出球O的半径,然后带入表面积公式即可。
易错点
不知道球心O在面ABC内的射影的位置;不会构建平面几何的知识求解半径。
知识点
21.若函数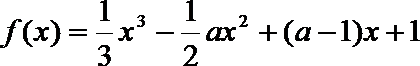
正确答案
函数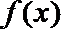
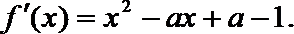
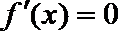
为增函数.
依题意应有 当
所以 
所以a的取值范围是[5,7].
解析
解析已在路上飞奔,马上就到!
知识点
10.已知A,B,C是球面上三点,且AB=6,BC=8,AC=10,球心O到平面ABC的距离等于该球半径的
正确答案
解析
△ABC的外接圆半径为5,且圆心在AC的中点处,又球心O到平面ABC的距离等于该球半径R的


考查方向
解题思路
先根据题目条件,画出图形,找到球心,再构造直角三角形,根据勾股定理计算出球的半径。
易错点
1、本题在确定球的球心时容易发生错误 。2、本题不容易找到球心的位置,导致题目无法进行。
知识点
设地球半径为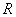
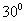
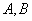
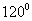
正确答案
解析
略
知识点
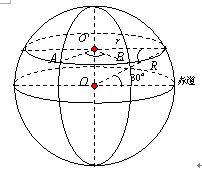
如图,半径为
















正确答案
解析
以O为原点,分别以OB、OC、OA所在直线为x、y、z轴,则
A
知识点
某几何体的三视图如图所示,则这个几何体的体积是() 。
正确答案
解析
略
知识点
扫码查看完整答案与解析