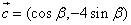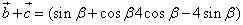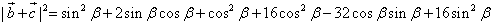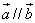- 数量积判断两个平面向量的垂直关系
- 共68题
已知向量
正确答案
6
解析
因为


知识点
15. 已知圆





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知:向量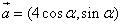
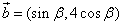
(1)若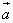
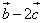
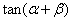
(2)求:
(3)若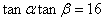
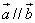
正确答案
(1)由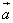
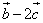
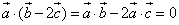
即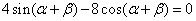
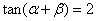
(2)
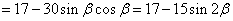
最大值为32,所以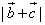
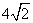
(3)由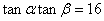
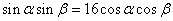
即 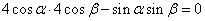
所以
解析
解析已在路上飞奔,马上就到!
知识点
21.已知平面向量a=(

(1)证明a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+ (t2–3)b,y=–ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况。
正确答案
(1)证明:∵a·b=
(2)解:∵x⊥y,∴x·y=0
即[a+(t2–3)b]·(–ka+tb)=0,整理后得
–ka2+[t–k(t2–3)]a·b+t(t2–3)·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t(t2–3)=0,∴k=
(3)解:讨论方程

于是f′(t)=

令f′(t)=0,解得t1=–1,t2=1.当t变化时,f′(t),f(t)的变化情况如下表:
当t=–1时,f(t)有极大值,f(t)极大值=
当t=1时,f(t)有极小值,f(t)极小值=–
而f(t)=


所以f(t)的图象大致如下:
于是当k>

当k=



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析