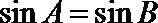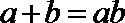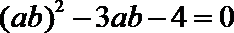- 数量积判断两个平面向量的垂直关系
- 共68题
1
题型:
单选题
|
4.设





正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
命题的真假判断与应用平行向量与共线向量数量积判断两个平面向量的垂直关系
1
题型:
单选题
|
3.设




正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
数量积的坐标表达式数量积判断两个平面向量的垂直关系
1
题型:填空题
|
13.已知









正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
数量积判断两个平面向量的垂直关系椭圆的几何性质
1
题型:
单选题
|
10.已知向量→OA=(4,6),→OB=(3,5),且→OC⊥→OA,→AC∥→OB,则向量→OC= ( )
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
平行向量与共线向量平面向量的坐标运算数量积判断两个平面向量的垂直关系
1
题型:简答题
|
19. 设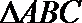
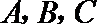
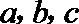
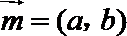
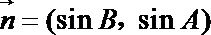
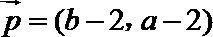
(1)若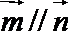
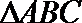
(2)若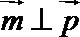
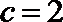
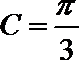
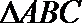
正确答案
设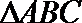
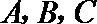

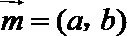
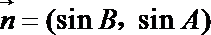
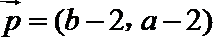
(1)若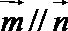
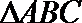
(2)若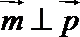
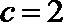
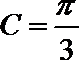
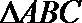
证明:(证法一)(1)∵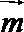
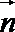
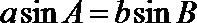
由正弦定理可知,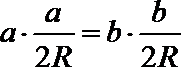
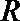
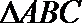
∴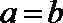

(证法二)∵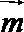
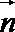
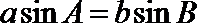
由正弦定理可知,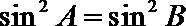
∵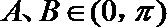
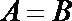
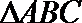
(2)由题意可知,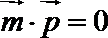
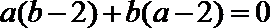
由余弦定理可知,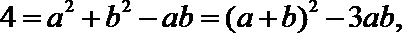


∴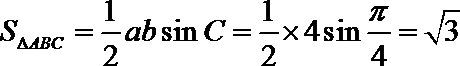
解析
解析已在路上飞奔,马上就到!
知识点
平面向量共线(平行)的坐标表示数量积判断两个平面向量的垂直关系
下一知识点 : 平面向量数量积坐标表示的应用
扫码查看完整答案与解析