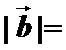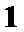- 数量积判断两个平面向量的垂直关系
- 共68题
1
题型:
单选题
|
4.向量


正确答案
B
解析
由










考查方向
本题主要考查向量的数量积的运算和向量的夹角等知识,意在考查考生的运算求解能力。
解题思路
先根据题意得到

易错点
不会根据

知识点
平面向量数量积的运算数量积表示两个向量的夹角数量积判断两个平面向量的垂直关系
1
题型:
单选题
|
4.已知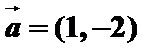
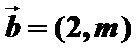
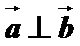
正确答案
D
解析
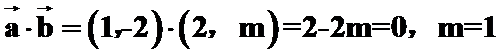
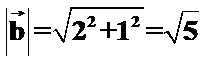
考查方向
本题主要考查了向量垂直的坐标表示和向量的模。
解题思路
先根据垂直数量积为零求出未知参数m,再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式 。
知识点
向量的模数量积判断两个平面向量的垂直关系
1
题型:填空题
|
14.已知|






正确答案
解析
因为

考查方向
数量积表示两个向量的夹角;平面向量数量积的运算
解题思路
先根据向量的数量积的定义,再根据向量垂直的性质求λ的值
易错点
平面向量及其应用
知识点
平面向量数量积的运算数量积判断两个平面向量的垂直关系
1
题型:填空题
|
14.已知|






正确答案
解析
由题意可得
再根据向量

求得
故答案为
考查方向
本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于中档题.
解题思路
由题意利用两个向量的数量积的定义求得
再根据向量


易错点
两个向量垂直,数量积为0.
知识点
平面向量数量积的运算数量积判断两个平面向量的垂直关系
1
题型:
单选题
|
5. 已知向量



A .
正确答案
B
解析




考查方向
向量的坐标运算,以及向量垂直的条件。
解题思路
利用向量垂直的条件:两向量数量积为零,利用向量坐标运算求数量积
易错点
熟悉向量数量积的坐标运算,向量垂直的条件。
知识点
平面向量数量积的运算数量积判断两个平面向量的垂直关系
下一知识点 : 平面向量数量积坐标表示的应用
扫码查看完整答案与解析