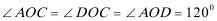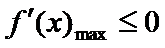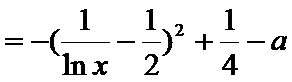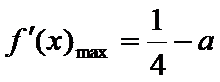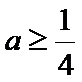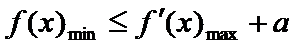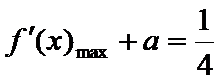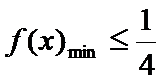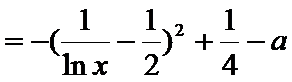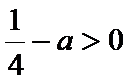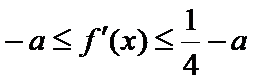- 直线与圆、圆与圆的位置关系
- 共468题
6．哈尔滨文化公同的摩天轮始建于2003年1月15日，2003年4月30日
竣工，是当时中国第一高的巨型摩天轮．其旋转半径50米，最高点距地
面110米，运行一周大约21分钟．某人在最低点的位置坐上摩天轮，则
第14分钟时他距地面大约为（）米．
正确答案
解析
如图，
根据周期可知第14分钟时从最低点A处转到了D处，D点距离地面
距离为：AB+10（米）由图知AB=50+25=75（米）
则第14分钟时他距地面大约为85米
故选B
考查方向
解题思路
1、根据题意建立圆模型，利用圆中的知识计算高度。
2、在圆中计算出结果后再加上10米。
易错点
1、本题易在建立圆模型上出错。
2、本题易忽视摩天轮最低点距地面的高度10米。
知识点
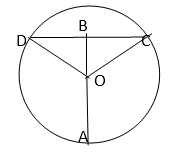
21．已知函数f（x）＝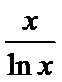
（Ⅰ）若函数f（x）在（1，＋∞）上是减函数，求实数a的最小值；
（Ⅱ）已知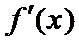
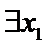
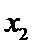
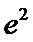
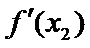
正确答案
（1）
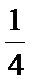
（2）
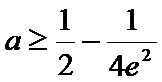
解析
解答过程如下：
（1）由已知得函数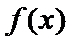
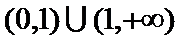
而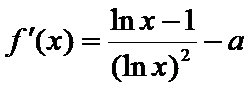
∴
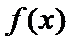
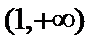
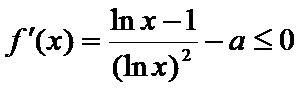
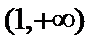
∴当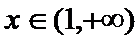
由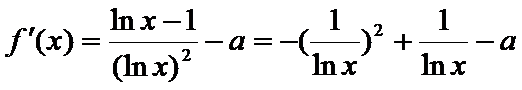
∴当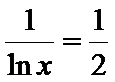
∴
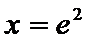
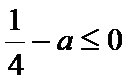
所以实数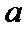
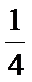
（2）若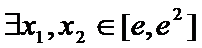
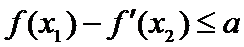
则有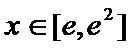
由（1）知 当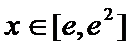
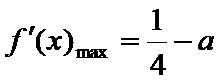
由此问题转化为：当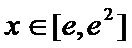
①当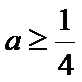
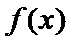
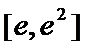
则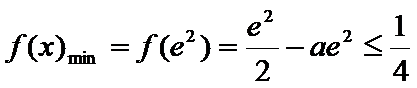
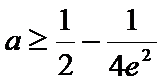
②当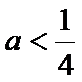
由于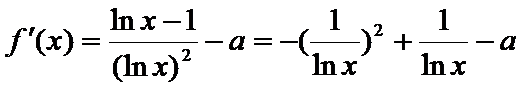
在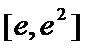
所以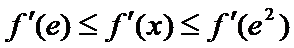
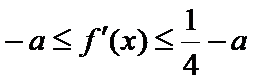
若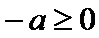
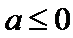
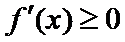
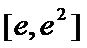
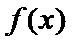
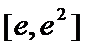
所以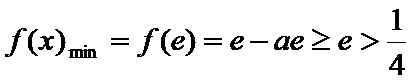
若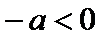
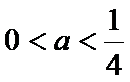
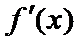
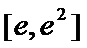
所以存在唯一的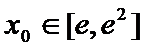
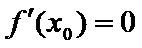
当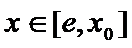
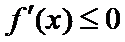
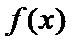
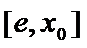
当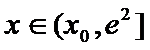
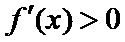
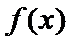
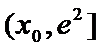
所以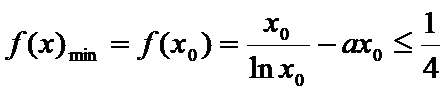
∴
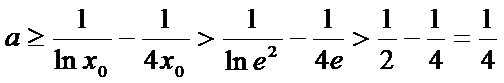
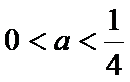
综上，得实数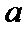
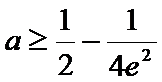
考查方向
解题思路
1、第（1）问可以通过函数的单调性与导数的关系，利用导数判断函数的单调性，再结合函数的单调性确定a的取值范围；
2、第（2）问可以通过转化化归的方法，将问题转化为函数的最大、最小值问题进行求解。
易错点
试题分析：本题第（1）问属于用导数研究函数的性质的问题，是导数题目中的常见问题；第（2）问是用导数作为工具来解决不等式问题，题目综合性较强，难度较大。
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，泽宇性别有关联的可能性最大的变量是（ ）
A成绩
B视力
C智商
D阅读量
正确答案
解析
表1：X2=
表2：X2=
表3：X2=
表4：X2=
∴阅读量与性别有关联的可能性最大
知识点
已知
A
B
C
D
正确答案
解析
由反函数的性质原函数的值域为反函数的定义域，原函数的定义域为反函数的值域。
当
知识点
学校游园活动有这样一个游戏项目：甲箱子里装有
（1）求在
(ⅰ) 摸出
(ⅱ) 获奖的概率；
（2）求在
正确答案
见解析
解析
（1） (ⅰ)设“在
(ⅱ)设“在
因为
（2） 
所以
数学期望
知识点
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )
A6
B6
C4
D4
正确答案
解析
该几何体是如图所示的棱长为4的正方体内的三棱锥E CC1D1(其中E为BB1的中点)，其中最长的棱为D1E＝＝6.
知识点
行列式
正确答案
6
解析
知识点
2010年上海世博会园区每天9:00开园，20:00停止入园。在右边的框图中，
正确答案
S 
解析
略
知识点
扫码查看完整答案与解析