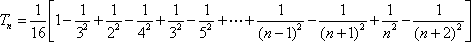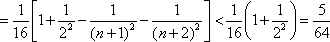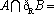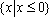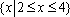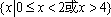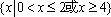- 直线与圆、圆与圆的位置关系
- 共468题
16.已知直线



正确答案
4
知识点
5.平行于直线

正确答案
解析
设所求切线方程为




考查方向
解题思路
先设出与已知直线平行的直线方程,再根据直线与圆相切时的位置关系列出等式,求出所设直线方程中的未知量。
易错点
计算过程中容易出错,点到直线的距离公式中,有绝对值,所以解有两种情况。
知识点
20. 椭圆C1:

( I )求C1的标准方程;
(Ⅱ)求四边形ABCD的面积的最大值.
正确答案
(1)
解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时选通过已知条件确定椭圆方程,再根据直线方程计算弦长,最后再求出面积,再利用分式函数最值求法求出最值。
(1)由题意
所以
(2) ①直线



设圆心


整理得
②当直线
当直线
综上,四边形
考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:
1、根据题意求出椭圆方程。
2、设AB、CD直线方程与椭圆联立求出弦AB、CD的长再利用面积公式计算面积。 3、利用分式函数求最值的方法求出最值。
易错点
1、不分直线斜率是否为0而丢分。
2、联立方程和求弦长时容易在运算上出错。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
正项数列{an}的前n项和Sn满足: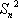
(1)求数列{an}的通项公式an;
(2)令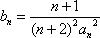
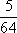
正确答案
见解析
解析
(1)解:由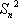
由于{an}是正项数列,所以Sn>0,Sn=n2+n.
于是a1=S1=2,n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
综上,数列{an}的通项an=2n.
(2)证明:由于an=2n,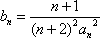
则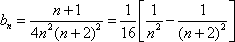
知识点
已知全集为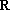
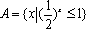
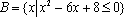
正确答案
解析
略
知识点
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )。
正确答案
解析
圆C1,C2的圆心分别为C1,C2,由题意知|PM|≥|PC1|-1,|PN|≥|PC2|-3,∴|PM|+|PN|≥|PC1|+|PC2|-4,故所求值为|PC1|+|PC2|-4的最小值,又C1关于x轴对称的点为C3(2,-3),所以|PC1|+|PC2|-4的最小值为|C3C2|-4=
知识点
设{an}是有正数组成的等比数列,

正确答案
解析
由a2a4=1可得





知识点
设


正确答案
解析
约束条件对应四边形

知识点
设函数
(1)求
(2)讨论关于

正确答案
见解析。
解析
(1)
令


所以



(2)令
①当

在











②当










由①②得,函数



当


当


当


知识点
扫码查看完整答案与解析