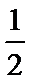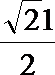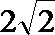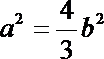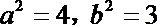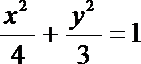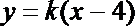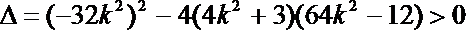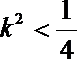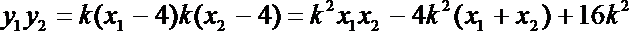- 直线与圆、圆与圆的位置关系
- 共468题
14.当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知下列五个命题:
①若一个圆锥的底面半径缩小到原来的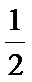
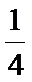
②若两组数据的中位数相等,则它们的平均数也相等;
③直线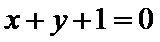
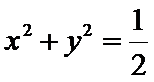
④“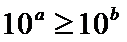
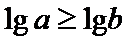
⑤过M(2,0)的直线l与椭圆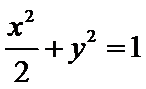
其中真命题的序号是:
正确答案
①③⑤
解析
解析已在路上飞奔,马上就到!
知识点
5.将直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知P(x,y)是直线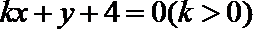
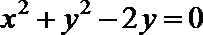
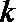
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 定义F(x,y)=(1+x)
(Ⅰ)令函数f(x)=F(1,log





(Ⅱ)当x,y∈N
正确答案
(Ⅰ) ∵ F(x,y)=(1+x)
∴ f(x)=F(1,log2(x2-4x+9))=2
f′(x)=2x-4,过O作C
∴ 
∴ S=


(Ⅱ)证明:令h(x)=

令P(x)=
∴P′(x)=
∴ P(x)在[0,+∞)上单调递减。
∴ 当x>0时,有P(x)<P(0),∴ 当x≥1时有h′(x)<0
∴ h(x)在[1,+∞)上单调递减。
∴ 1≤x<y时,有
yln(1+x)>x ln(1+y)
∴ (1+x)
∴ 当x,y∈N
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆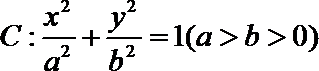

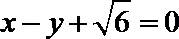
(1)求椭圆C的方程;
(2)求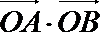
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
正确答案
(1)解:由题意知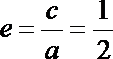
∴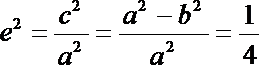
又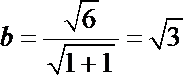
∴
故椭圆的方程为
(2)解:由题意知直线l的斜率存在,设直线l的方程为
由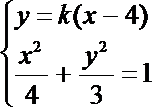
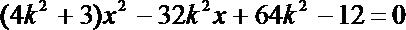
由
得:
设A(x1,y1),B (x2,y2),则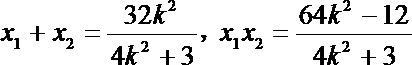
∴
解析
解析已在路上飞奔,马上就到!
知识点
14.在平面直角坐标系中,定义






正确答案

解析
解析已在路上飞奔,马上就到!
知识点
3.已知圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析