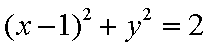直线与圆、圆与圆的位置关系
共468题

直线与圆、圆与圆的位置关系
共468题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

4．“C=5”是“点(2，1)到直线3x+4y十C=0的距离为3”的( )

A充要条件

B充分不必要条件

C必要不充分条件

D既不充分也不必要条件

正确答案

解析

由题意知点到直线的距离为3等价于，解得或，所以“”是“点到直线的距离为3”的充分不必要条件，故A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查了点到直线的距离公式及充分必要条件的定义，考查考生对定义的理解及运算能力。

解题思路

先求出点(2，1)到直线3x+4y十C=0的距离为3的充要条件的C的值为或，再进行判断。故A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

采用代入验证出错。

知识点

充要条件的判定直线与圆的位置关系直线和圆的方程的应用

题型：填空题

填空题 · 5 分

14. 已知圆，过点的直线交该圆于两点，为坐标原点，则面积的最大值是．

正确答案

解析

当直线的斜率不存在时，由题可得的面积为0；当直线的斜率存在时，由题可设其斜率为k,则直线的方程为，即，所以圆心到直线的距离，，令，所以

，所以，面积的最大值为。

考查方向

本题主要考查了直线圆的位置关系、垂径定理、点到直线的距离公式，同时也考查了考生分类讨论思想和利用配方法求函数最值的能力。

解题思路

讨论直线的斜率存在与不存在两种情况，当斜率存在时，设出其方程，并求出圆心到直线的距离d，从而得到的面积，再利用换元，配方法即可得出结论。

易错点

本题易在求面积的最大值时发生错误。

知识点

直线与圆的位置关系直线和圆的方程的应用

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 5 分

已知等比数列｛an｝为递增数列，且，则数列｛an｝的通项公式an =______________。

正确答案

解析

知识点

圆与圆的位置关系及其判定

题型：简答题

简答题 · 14 分

如图，在三棱锥中，分别为棱的中点，已知。

（1）求证：直线PA∥平面DEF；

（2）平面BDE⊥平面ABC。

正确答案

见解析。

解析

本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系，考查空间想象能力和推理论证能力。

（1）∵为中点 ∴DE∥PA

∵平面DEF，DE平面DEF ∴PA∥平面DEF

（2）∵为中点 ∴

∵为中点 ∴

∴ ∴，∴DE⊥EF

∵，∴

∵ ∴DE⊥平面ABC

∵DE平面BDE， ∴平面BDE⊥平面ABC。

知识点

圆与圆的位置关系及其判定

题型：填空题

填空题 · 5 分

一个几何体的三视图如图所示，则该几何体的表面积为______________。

正确答案

解析

由三视图可知该几何体为一个长方体在中间挖去了一个等高的圆柱，其中长方体的长、宽、高分别为4、3、1，圆柱的底面直径为2，所以该几何体的表面积为长方体的表面积加圆柱的侧面积再减去圆柱的底面积，即为

知识点

圆与圆的位置关系及其判定

题型：单选题

单选题 · 5 分

函数的图像与函数的图像的交点个数为

正确答案

解析

略

知识点

圆与圆的位置关系及其判定

题型：单选题

单选题 · 5 分

设是定义在R上的奇函数，当时，,则

A-3

B-1

正确答案

解析

略

知识点

圆与圆的位置关系及其判定

题型：简答题

简答题 · 12 分

如图，在平面直角坐标系xoy中，椭圆的离心率为，过椭圆由焦点F作两条互相垂直的弦AB与CD. 当直线AB斜率为0时，弦AB长4.

26.求椭圆的方程；

27.若直线AB斜率为1时，求弦AB长；

28.过椭圆的对称中心O，作直线L，交椭圆与M,N，三角形FMN是否存在在大面积？若存在，求出它的最大面积值。若不存在，说明理由

第(1)小题正确答案及相关解析

正确答案

当AB的斜率为0时，AB=半长轴，即

2a=4，a=2；

又因为 e=c/a，，故a=

又，故b2=1

所以解析式为

解析

看解题步骤

考查方向

圆锥曲线

解题思路

利用离心率公式。abc之间的关系

易错点

不要写成a2+b2=c2

教师点评

考查圆锥曲线解析式求解

第(2)小题正确答案及相关解析

正确答案

联立直线与椭圆方程得：5x2-8x=0设方程根为x1=0,x2=8/5,

|AB|==

解析

见答案

考查方向

直线与圆锥曲线的关系，两点之间的距离

解题思路

先求出两焦点的横坐标，利用距离与斜率、求两点间的距离公式求解

易错点

无

教师点评

考查了直线与圆锥曲线的关系，和用斜率求两点距离

第(3)小题正确答案及相关解析

正确答案

S⊿FMN= ≤(当M在顶点时，面积最大，)

题型：填空题

填空题 · 5 分

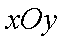
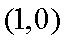
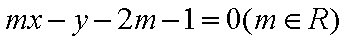
10.在平面直角坐标系中，以点为圆心且与直线相切的所有圆中，半径最大的圆的标准方程为__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程直线与圆的位置关系

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 直线与圆、圆与圆的位置关系

扫码查看完整答案与解析