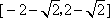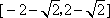正弦函数的定义域和值域
共98题

· 正弦函数的定义域和值域

正弦函数的定义域和值域
共98题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：单选题

单选题 · 5 分

若△的内角，满足，则（）.

正确答案

解析

，
由正弦定理知，

由余弦定理得 .

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 5 分

（几何证明选讲选做题）如图1，在平行四边形中，点E在上且,与交于点，则＝ .

正确答案

解析

略

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 12 分

已知函数。

（1）求函数的最小正周期和值域；

（2）若，求的值。

正确答案

（1）f（x）的最小正周期为2，值域为

（2）

解析

（1）由已知，f（x）=

所以f（x）的最小正周期为2，值域为。

（2）由（1）知，f（）=

所以cos（）。

所以

，

知识点

三角函数的周期性及其求法正弦函数的定义域和值域三角函数中的恒等变换应用二倍角的正弦二倍角的余弦

题型：简答题

简答题 · 12 分

设函数f(x)＝sin2ωx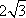＋sinωx·cosωx－cos2ωx＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈(，1)。

(1)求函数f(x)的最小正周期；

(2)若y＝f(x)的图象经过点(，0)，求函数f(x)的值域。

正确答案

(1) ;(2)

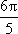
解析

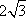
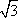
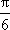
(1)因为f(x)＝sin2ωx－cos2ωx＋sinωx·cosωx＋λ＝－cos2ωx＋sin2ωx＋λ＝2sin(2ωx－)＋λ，

由直线x＝π是y＝f(x)图象的一条对称轴，可得sin(2ωπ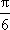－)＝±1.

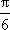
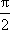
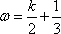
所以2ωπ－＝kπ＋(k∈Z)，即(k∈Z)。

又ω∈(，1)，k∈Z，所以.

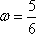
所以f(x)的最小正周期是.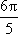

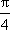
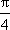
(2)由y＝f(x)的图象过点(，0)，得f()＝0，

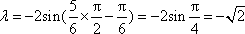
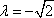
即，即.

故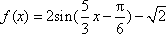，函数f(x)的值域为

知识点

正弦函数的定义域和值域由y=Asin（ωx+φ）的部分图象确定其解析式三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 正弦函数的单调性

百度题库 > 高考 > 文科数学 > 正弦函数的定义域和值域

扫码查看完整答案与解析