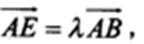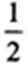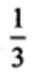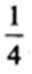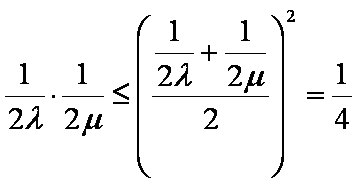正弦函数的定义域和值域
共98题

· 正弦函数的定义域和值域

正弦函数的定义域和值域
共98题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设与是定义在同一区间[a, b]上的两个函数，若函数上有两个不同的零点，则称和在[a, b]上是“联系函数”，区间[a, b]称为“联系区间”，若与在[0,3]上是“联系函数”，则k的取值范围为 ( )

正确答案

解析

依题意，令，则在上有两个零点，所以，即，则有

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 16 分

将圆按向量平移得到圆，直线与圆相交于、

两点，若在圆上存在点，使求直线的方程。

正确答案

见解析。

解析

由已知圆的方程为，

按平移得到.

∵∴.

即.

又，且，∴.∴.

设，的中点为D.

由，则，又.

∴到的距离等于.

即， ∴m=1

∴直线的方程为：或.

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

已知△ABC中，D是BC边的中点，过点D的直线分别交直线AB、AC于点E、F，若

的最小值是

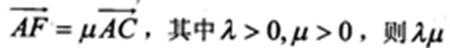
正确答案

解析

解析：由已知得：，,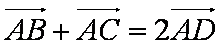

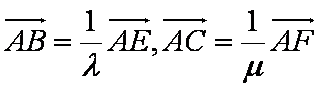
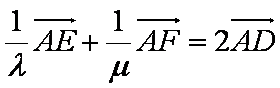
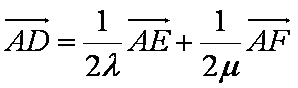
所以,即,

因为D,E,F三点共线，

所以，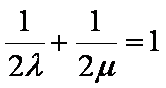

又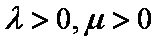，由基本不等式可得：

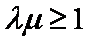
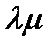
所以，即的最小值是1，

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

若函数（ω>0）在区间上单调递增，在区间上单调递减，则ω=（）

正确答案

解析

函数的周期,因为在区间上单调递增，在区间上单调递减,所以,.简单考查三角函数的图像和单调性,周期问题,是简单题.

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 8 分

已知，函数

（1）求的最小正周期，并求其图象对称中心的坐标；

（2）当时，求函数f(x)的值域.

正确答案

见解析。

解析

（1）

………2分

所以的最小正周期为

令，得。

故所求对称中心的坐标为- ………4分

（2） ………6分

即的值域为　　 - ………8分

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用数量积的坐标表达式

继续学习学习下一知识点

下一知识点 : 正弦函数的单调性

百度题库 > 高考 > 文科数学 > 正弦函数的定义域和值域

扫码查看完整答案与解析