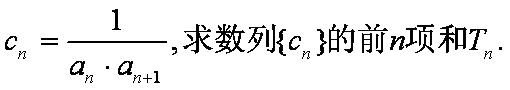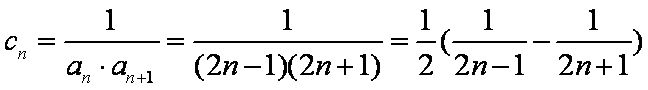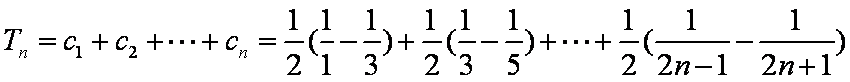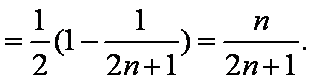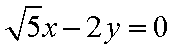正弦函数的定义域和值域
共98题

· 正弦函数的定义域和值域

正弦函数的定义域和值域
共98题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

已知等差数列

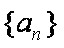
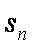
（1）求数列的通项公式，写出它的前n项和；

（2）求数列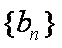的通项公式；

（3）若

正确答案

见解析。

解析

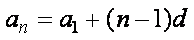
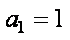
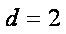
（1）设，由题意得，，

所以，；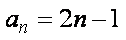

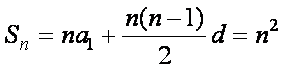
（2），，所以，，…… （）

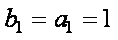
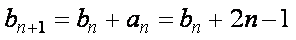
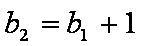
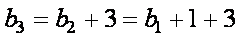
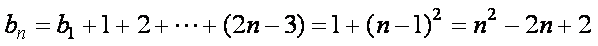
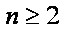
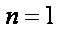
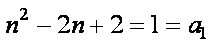
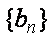
又时，所以数列的通项；

（3）

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 4 分

已知是椭圆和双曲线的公共焦点，是它们的一个公共点，且，则的最大值为

正确答案

解析

略

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

已知是定义在上的函数，下列命题正确的是 ( )

A若在区间上的图像是一条连续不断的曲线，且在内有零点，则有.

B若在区间上的图像是一条连续不断的曲线，且有，则其在内没有零点。

C若在区间上的图像是一条连续不断的曲线，且有，则其在内有零点。

D如果函数在区间上的图像是一条连续不断的曲线，且有，则其在区间内有零点。

正确答案

解析

略

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 5 分

在△ABC中，AC边上的高为BD，垂足为D，且||=，则•=　　。

正确答案

-3

解析

∵BD是AC边上的高，∴BD丄AC，

∴=0，

∵||=，

∴•=•（+）=•+•=0﹣2=﹣3。

故答案为：﹣3，

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 14 分

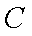
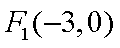
已知中心在原点的双曲线的一个焦点是，一条渐近线的方程是

（1）求双曲线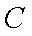的方程；

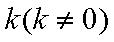
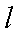
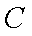
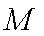
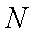
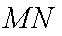
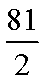
（2）若以为斜率的直线与双曲线相交于两个不同的点，，且线段的垂直平分线与两坐标轴围成的三角形的面积为，求的取值范围

正确答案

见解析

解析

（1）设双曲线的方程为， 1分

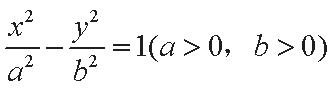
由题设得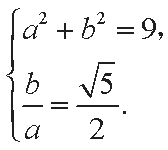 3分

解得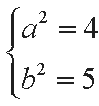， 5分

所以双曲线的方程为； 6分

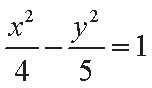
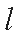
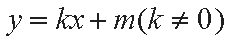
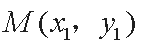
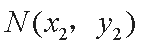
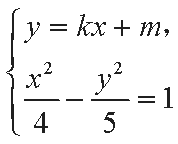
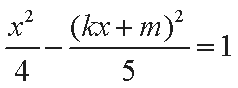
（2）设直线的方程为，点，的坐标满足方程组，将①式代入②式，得，

整理得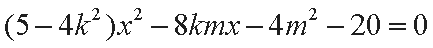， 8分

此方程有两个不等实根，于是，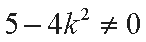

且，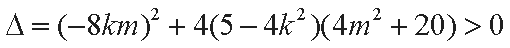

整理得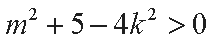，③ 9分

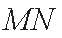
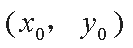
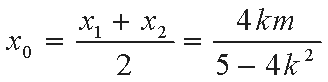
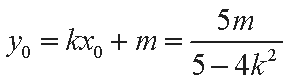
由根与系数的关系可知线段的中点坐标满足：

，， 10分

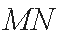
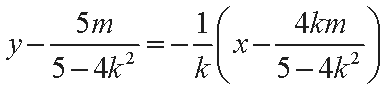
从而线段的垂直平分线的方程为， 1分

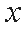
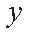
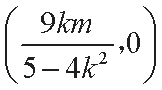
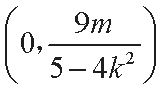
此直线与轴，轴的交点坐标分别为，，

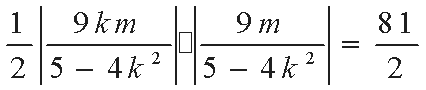
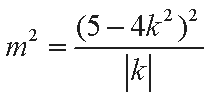
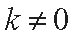
由题设可得，整理得，， 12分

将上式代入③式得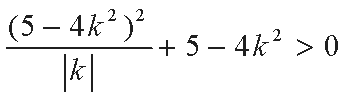， 13分

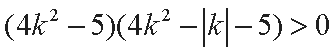
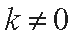
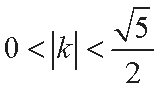
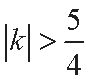
整理得，，解得或，

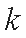
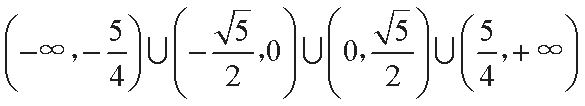
所以的取值范围是， 14分

知识点

正弦函数的定义域和值域

继续学习学习下一知识点

下一知识点 : 正弦函数的单调性

百度题库 > 高考 > 文科数学 > 正弦函数的定义域和值域

扫码查看完整答案与解析