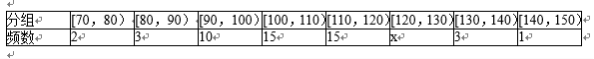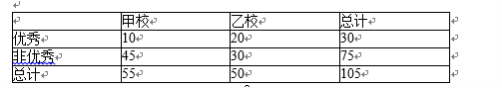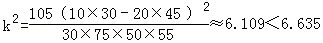- 独立性检验的应用
- 共14题
19.有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式:
参考数据:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸,呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机对入院50人进行了问卷调查,得到了如下的列联表.
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量
下面的临界值表供参考:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某人研究中学生的性别与阅读量的关系,随机抽查500名中学生,得到统计数据如下表:
附表:
参照附表,可得到的结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性。
(1) 根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率。
附:
正确答案
(1) 有关;(2)
解析
(1)
由频率分布直方图可知,在抽取的100人中,“体育迷”为25人,从而完成2×2列联表如下:
将2×2列联表中的数据代入公式计算,得

因为3.030<3.841,所以我们没有理由认为“体育迷”与性别有关。
(2)由频率分布直方图可知,“超级体育迷”为5人,从而一切可能结果所组成的基本事件空间为
Ω={(a1,a2),(a1,a3),(a2,a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}。
其中ai表示男性,i=1,2,3。bj表示女性,j=1,2。
Ω由10个基本事件组成,而且这些基本事件的出现是等可能的。
用A表示“任选2人中,至少有1人是女性”这一事件,则
A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},
事件A由7个基本事件组成,因而
知识点
某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀。
甲校:
乙校:
(1)求表中x与y的值;
(2)由以上统计数据完成下面2x2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
正确答案
见解析
解析
(1)由分层抽样可知,甲校抽取105×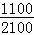
所以x=55﹣(2+3+10+15+15+3+1)=6,y=50﹣(1+2+9+8+10+10+3)=7;
(2)2x2列联表如下
所以
所以没有99%的把握认为学生数学成绩优秀与所在学校有关。
知识点
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名。
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率。
正确答案
见解析
解析
(1)由题意可得列联表:
因为
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系。
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表
分组的情况总有6中,工作人员甲负责收集数据且工作人员乙负责处理数据占两种,所以工作人员甲负责收集数据且工作人员处理数据的概率是
知识点
“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动,假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构

根据表中数据,能否有90%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:
正确答案
见解析
解析
(1)这3个人接受挑战分别记为

这3个人参与该项活动的可能结果为:







其中,至少有2个人接受挑战的可能结果有:




(2)根据


因为
知识点
大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下:
(1)试估计该校学生阅读莫言作品超过50篇的概率;
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”。根据题意完成下表,并判断能否有75%的把握认为对莫言作品的非常了解与性别有关?
附:
正确答案
见解析。
解析
(1)由抽样调查阅读莫言作品在50篇以上的频率为

(2)
根据列联表数据得

所以没有75%的把握认为对莫言作品的非常了解与性别有关.
知识点
17.某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有


(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下
①完成列联表;
②能否有
(3)若一班有





现从这
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.第12届全国人民代表大会于2013年3月在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和1 4名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
(I)根据以上数据完成以下2×2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
参考公式:
参考数据:
(II)会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随机抽取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析