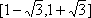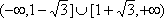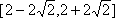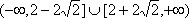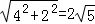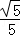- 导数与积分
- 共3028题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设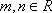
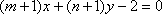
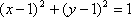
正确答案
解析
∵直线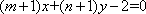
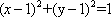
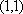
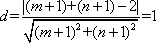
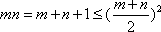
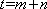
则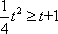
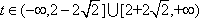
知识点
设A是由m×n个实数组成的m行n列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m,n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和(1≤ⅰ≤m),Cj(A)为A的第j列各数之和(1≤j≤n):
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 对如下数表A,求K(A)的值;
(2)设数表A∈S(2,3)形如
求K(A)的最大值;
(3)给定正整数t,对于所有的A∈S(2,2t+1),求K(A)的最大值。
正确答案
(1)
(2)
(3)
解析
(1)由题意可知



∴
(2)先用反证法证明
若
则
同理可知
由题目所有数和为
即
∴
与题目条件矛盾
∴
易知当

∴
(3)

首先构造满足



经计算知,



下面证明


由







设





考虑






故



知识点
在平面直角坐标系中,点0(0,0),P(6,8),将向量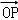
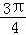
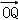
正确答案
解析
∵点0(0,0),P(6,8),
∴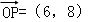
设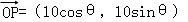
则cosθ=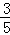

∵向量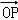
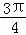
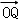
∴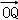
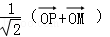
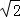
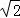
知识点
设a,b∈R.“a=O”是‘复数a+bi是纯虚数”的( )
正确答案
解析
当




知识点
在△ABC中,若α=2,b+c=7,

正确答案
4
解析
在△ABC中,利用余弦定理



知识点
某地区有小学150所,中学75所,大学25所.现采用分层抽样的方法从这些学校中抽取30所学校
对学生进行视力调查,应从小学中抽取_________所学校,中学中抽取________所学校。
正确答案
18,9
解析
∵分层抽样也叫按比例抽样,由题知学校总数为250所,所以应从小学中抽取

知识点
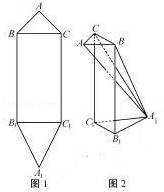
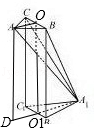
平面图形ABB1A1C1C如图1所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC=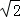
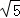
(1)证明:AA1⊥BC;
(2)求AA1的长;
(3)求二面角A﹣BC﹣A1的余弦值。
正确答案
见解析
解析
(1)证明:取BC,B1C1的中点为点O,O1,连接AO,OO1,A1O,A1O1,
∵AB=AC,∴AO⊥BC
∵平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC
∴AO⊥平面BB1C1C
同理A1O1⊥平面BB1C1C,∴AO∥A1O1,∴A、O、A1、O1共面
∵OO1⊥BC,AO⊥BC,OO1∩AO=O,∴BC⊥平面OO1A1A
∵AA1⊂平面OO1A1A,∴AA1⊥BC;
(2)解:延长A1O1到D,使O1D=OA,则∵O1D∥OA,∴AD∥OO1,AD=OO1,
∵OO1⊥BC,平面A1B1C1⊥平面BB1C1C,平面A1B1C1∩平面BB1C1C=B1C1,
∴OO1⊥面A1B1C1,
∵AD∥OO1,
∴AD⊥面A1B1C1,
∵AD=BB1=4,A1D=A1O1+O1D=2+1=3
∴AA1=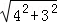
(3)解:∵AO⊥BC,A1O⊥BC,∴∠AOA1是二面角A﹣BC﹣A1的平面角
在直角△OO1A1中,A1O=
在直角△OAA1中,cos∠AOA1=﹣
∴二面角A﹣BC﹣A1的余弦值为﹣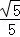
知识点
右图是求样本



正确答案
解析
略
知识点
扫码查看完整答案与解析