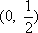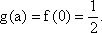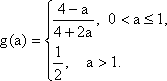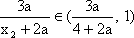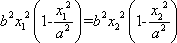- 导数与积分
- 共3028题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知


(1)求a的值;
(2)若
正确答案
见解析
解析
(1)由



当
当


(2)记

所以

知识点
已知函数

正确答案
解析
得:


知识点
已知P,Q为抛物线

正确答案
-4
解析
因为点P,Q的横坐标分别为4,
由


知识点
已知
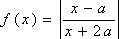
(1)记

(2)是否存在
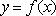
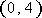

正确答案
(1)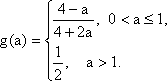
解析
(1)当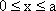
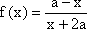
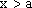
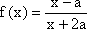
当
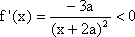
当
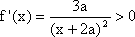

① 若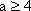
② 若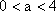
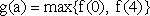
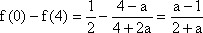
当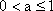
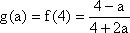
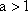
综上所述,
(2) 由(I)可知,若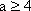
当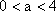
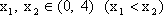
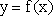
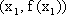
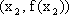
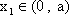
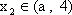
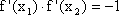
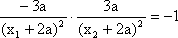
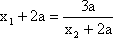
由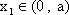
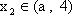
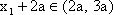
故(*)成立等价于集合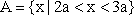
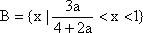
因为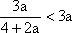
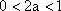
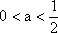
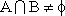
综上所述,存在

知识点
在

(1)求证:
(2)若
正确答案
见解析
解析
(1)先将
(2)由


知识点
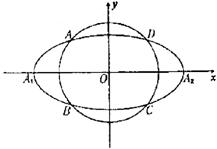
如图,椭圆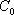
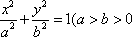
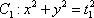
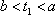
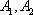
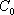
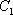
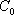
(1)求直线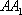
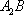
(2)设动圆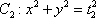
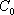
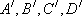
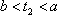
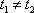
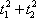
正确答案
见解析
解析
(1)设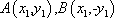
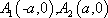
直线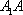
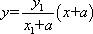
直线
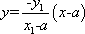
由①②得 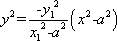
由点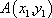
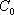
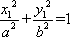
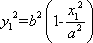
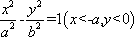
(2)证明:设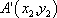
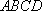
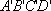
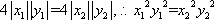
由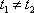
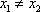
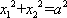
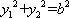
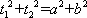
知识点
已知等比数列


(1)求数列
(2)是否存在正整数


正确答案
见解析
解析
(1)设等比数列{an}的公比为q,则由已知可得
解得
故
(2)若




从而
=
若an=(-5)·(-1)n-1,则




综上,对任何正整数m,总有
故不存在正整数m,使得
知识点
设


(1)
(2)
正确答案
(1) 
解析
略
知识点
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )。
正确答案
解析
解析:函数f(x)的图象有以下三种情形:


a=0 a>0 a<0
由图象可知f(x)在区间(0,+∞)内单调递增时,a≤0,故选C.
知识点
扫码查看完整答案与解析