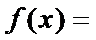- 导数与积分
- 共3028题
若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b= 。
正确答案
知识点
设直线l1,l2分别是函数f(x)= 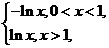
正确答案
知识点
15.已知f(x)为偶函数,当

正确答案
知识点
已知函数
24.设


25. 若对于任意


26.若



正确答案
解析



则



考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析
由题意得
令


此时

∵


因此实数

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析


由




而


因此







则




① 若








因此









则
② 若



可得
由
因此
因此


因此

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
已知函数
24.证明:当
25.证明:当

26.确定k的所以可能取值,使得存在


正确答案
(Ⅰ)详见解析
解析
解法一:(1)令
当



故当



考查方向
解题思路
求导,然后分类讨论求单调性
易错点
导数和函数的关系掌握不牢,不会利用导数判断函数的单调性
正确答案
(Ⅱ)详见解析
解析
(2)令

当



故对任意正实数
当


取






综上,当



考查方向
解题思路
先构造函数,然后求导判断单调区间,利用函数的单调性证明不等式。
易错点
不会构造函数,不会建立函数与导数之间的联系
正确答案
(Ⅲ) 
解析
(3)当



令
则有
故当





当



此时
令
则有
故当



故




则当
当

令
当




故当

综上,
考查方向
解题思路
分K大于1.K小于1和K等于1把不等式的左边去掉绝对值,然后再进行分类讨论,可得答案。
易错点
计算能力弱,求导分类讨论或重或漏
16.若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b= 。
正确答案
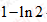
知识点
已知函数

27. 讨论
28. 设曲线




29. 若关于


正确答案
(I) 当









解析
(I)解:由






下面分两种情况讨论:
(1)当
令


当


-
+
-
所以,




当


当


所以,


考查方向
解题思路
利用导数的运算、导数的几何意义解答。
易错点
不会分类讨论。
正确答案
(II)见解析;
解析
(II)证明:设点










由于















考查方向
解题思路
利用导数研究函数的性质、证明不等式等基础知识和方法.
易错点
不会利用导数的几何意义来解答。
正确答案
(III)见解析.
解析
(III)证明:不妨设








类似地,设曲线






设方程






由此可得
因为


所以,
考查方向
解题思路
分类讨论思想、函数思想和划归思想,综合分析问题和解决问题的能力。
易错点
难度大做不出来。
设函数

26.讨论函数
27.若


正确答案
当

当

当

解析
(Ⅰ)由题意知 函数


令
(1)当

此时


(2)当

①当





②当

设方程

因为
所以
由 

所以 当


当


当


因此 函数有两个极值点。
(3)当

由

当


当


所以函数有一个极值点。
综上所述:
当

当

当

考查方向
解题思路
(I)函数f(x)=ln(x+1)+a(x2﹣x),其中a∈R,x∈(﹣1,+∞).
(2)当a>0时,△=a(9a﹣8).①当

(3)当a<0时,△>0.即可得出函数的单调性与极值的情况.
易错点
分类讨论函数取得极值的情况,注意函数单调性的制约作用。
正确答案
(Ⅱ)
解析
(II)由(I)知,
(1)当


因为 
所以 

(2)当


所以 函数

又


(3)当


所以

因为
所以

(4)当

因为
所以 

因此 当

即
可得 
当

此时 
综上所述,
考查方向
解题思路
(II)由(I)可知:(1)当
(2)当
(3)当1<a时,由g(0)<0,可得x2>0,利用x∈(0,x2)时函数f(x)单调性,即可判断出;
(4)当a<0时,设h(x)=x﹣ln(x+1),x∈(0,+∞),研究其单调性,即可判断出
易错点
利用导数研究函数恒成立问题,注意转化与化归思想的应用.菁优网版权所有
设函数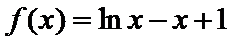
25.讨论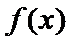
26.证明当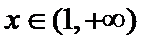
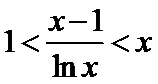
27.设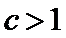
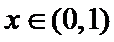
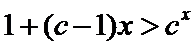
正确答案
(Ⅰ)当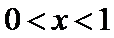
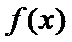
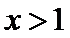
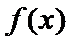
解析
(I)由题设,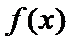
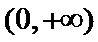
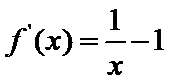
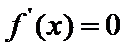
当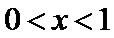
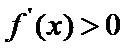
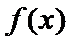
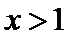
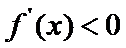
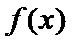
考查方向
解题思路
(I)首先求出导函数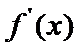
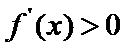
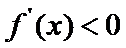
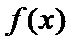
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,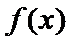
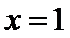
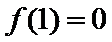
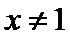
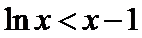
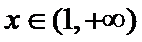
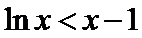
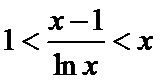
解析
(II)由(I)知,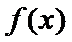
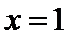
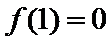
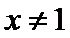
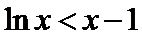
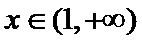
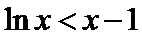
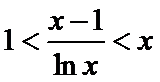
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的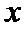

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设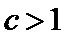
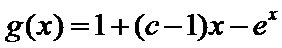
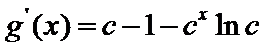
解得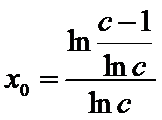
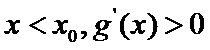
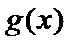
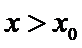
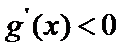
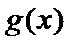
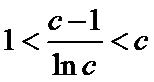
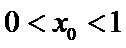
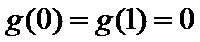
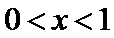
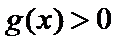
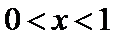
解析
(III)由题设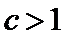
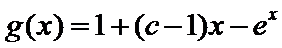
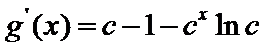
解得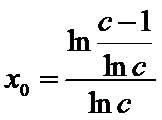
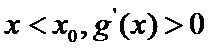
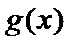
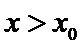
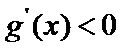
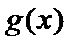
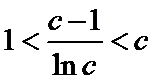
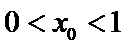
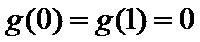
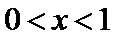
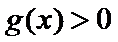
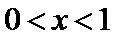
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
(本小题满分13分)
已知函数
(Ⅰ)求函数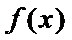
(Ⅱ)当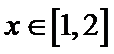
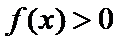
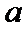
(Ⅲ)试问过点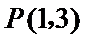
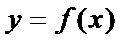
正确答案
考查方向
易错点
1、第一问在对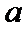
知识点
扫码查看完整答案与解析