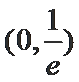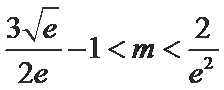- 导数与积分
- 共3028题
12.设定义在




正确答案
解析
f(x)的定义域为
因为
所以
所以
所以
所以f(x)在区域内单调递增,所以既无极大值也无极小值
考查方向
利用导数求函数的极值
解题思路
先求定义域,然后求导,然后判断函数单调性
然后求出函数的极值
易错点
求导错误,判断极值时错误
教师点评
有极大值不一定有最大值,有最大值也不一定有极大值
知识点
已知函数
25.当

26.当


正确答案
令



故
解析
参见答案,注意适当的放缩不等式。
考查方向
不等式、函数、导数结合题,利用导数判断函数的单调性,进而证明不等式
解题思路
先构造正确的函数,然后对函数求导,求导后求出函数的单调区间,利用函数的单调性证明不等式。
易错点
不能够造出正确的函数,求导错误,算单调区间错误。
教师点评
本题的关键在于构造出正确的函数,然后求导利用函数单调性方可证明不等式
正确答案
当


当

所以

令
令
当

令




因此


所以,当

当

令




因此,


所以,当

综上,当



解析
详见答案,构造不等式函数时要适当
考查方向
函数导数不等式的综合题,不等式恒成立求参数的取值范围
解题思路
根据x的不同取值,将不等式化简变形,够造出新的函数,然后求导判断单调区间,利用单调性证明不等式,利用不等式恒成立,再讨论参数K的取值范围。
易错点
分类讨论有重复或有遗漏,计算错误。判断函数符号错误
教师点评
主要是构造出正确的不等式(函数)形式,本题的难点在于分类讨论时,要综合考虑所有的情况。
已知函数


25.求实数
26.用




正确答案
详见解析
解析
(1)对

设直线



解得

考查方向
导数的几何意义 利用导数求曲线的切线
解题思路
对
易错点
求导错误,想不到利用导数求曲线的切线
教师点评
导数是求曲线的切线的一个工具
正确答案
详见解析
解析
(2)记函数

对函数

当

当

从而
∴



∵

又曲线



∴
∴
从而
∴
由函数





①当




记

当


∴
故“



②当




综合(1)(2)知,当

故实数

考查方向
导数与函数的综合题,利用导数求函数的单调性
利用函数和导数证明不等式
解题思路
先利用导数判断函数的单调性及单调区间,利用函数的零点存在性定理及其单调性,分类讨论x的不同取值,进而判断实数C的取值范围
易错点
计算能力弱,求导错误,不能构造出恰当的函数
教师点评
这类题根据题意和已知条件,按逻辑分类讨论相关参数的值,最后综合所有出现的可能情况,得到答案
已知函数



24.当

25.若


正确答案
略
正确答案
略
(本小题满分14分)
设函数f(x)=ax2-a-lnx,其中a
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得f(x) >
正确答案
知识点
已知函数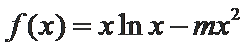
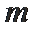
25.当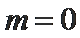
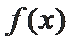
26.若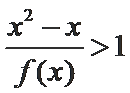
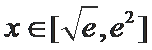
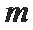
27.若
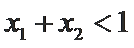
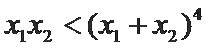
正确答案
当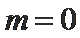
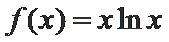
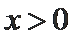
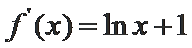
由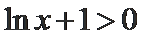
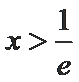
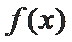
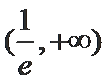
由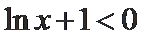
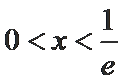
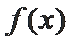
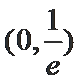
∴综上,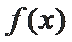
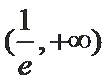
解析
当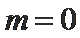
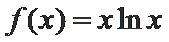
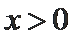
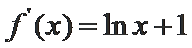
由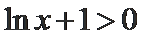
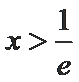
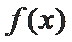
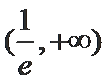
由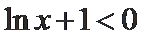
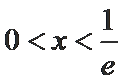
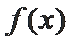
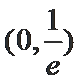
∴综上,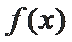
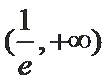
考查方向
本题主要考查了导数的应用——利用导数求函数的单调区间问题,属于常规性问题。
解题思路
首先将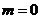
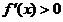
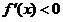
易错点
本题容易因含有对数的超越不等式不会解而导致结果算不出来。
教师点评
本题属于常规性问题,在每一年的高考中都会考到,需要考生加强这一类问题的训练。
正确答案
已知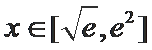
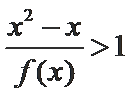
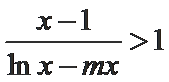
从而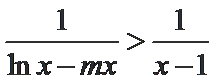
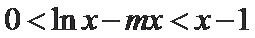
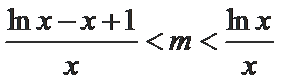
令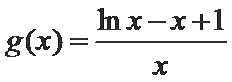
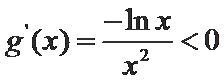
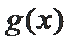
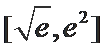
∴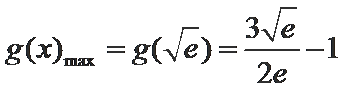
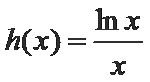
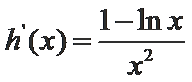
当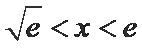
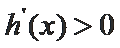
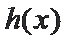
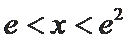
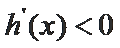
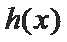
而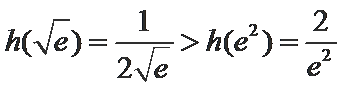
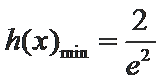
解析
已知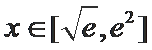
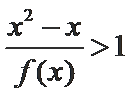
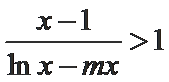
从而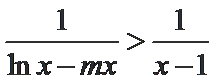
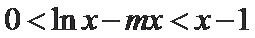
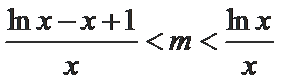
令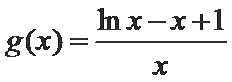
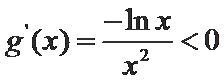
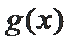
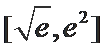
∴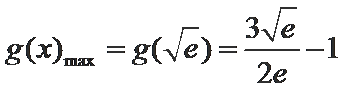
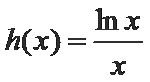
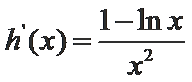
当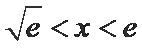
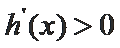
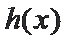
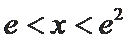
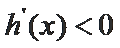
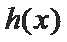
而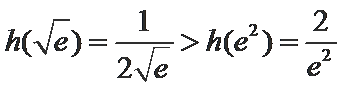
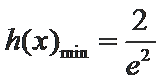
考查方向
本题主要考查了导数的应用,通过求最值来解决不等式恒成立的问题。
解题思路
首先将问题转化为求函数的最值的问题,然后在利用导数予以解决。
易错点
本题在对恒成立问题的分析中容易产生错误的理解而导致出错。
正确答案
由(1)知,当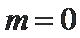
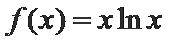
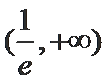
∵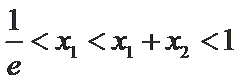
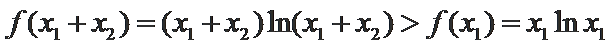
即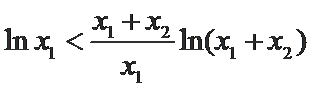
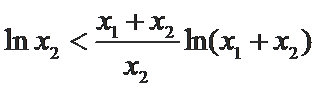
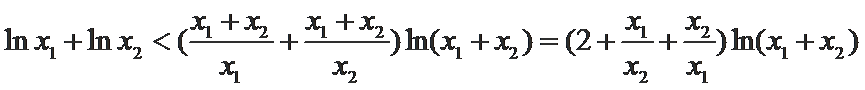
又因为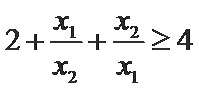
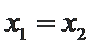
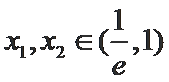
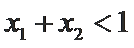
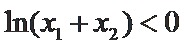
∴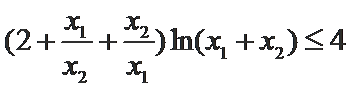
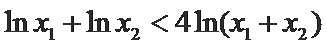
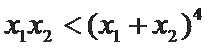
解析
由(1)知,当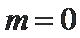
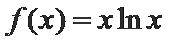
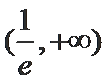
∵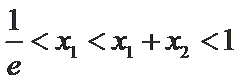
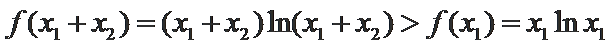
即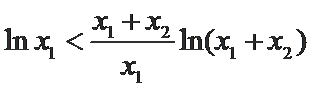
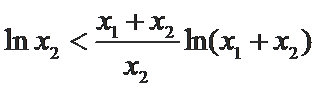
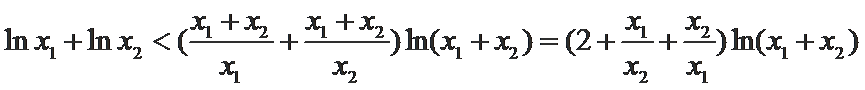
又因为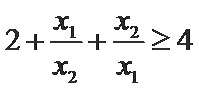
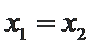
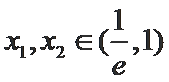
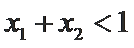
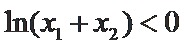
∴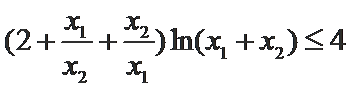
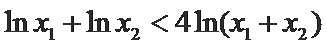
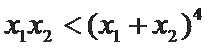
考查方向
本题考查了导数的应用以及不等式的证明。
解题思路
首先根据函数的单调性予以放缩,再利用放缩法予以证明。
易错点
本题容易因为放缩法掌握不清楚而导致出现错误。
教师点评
本题属于不等式的证明问题,难度较大,考生需要有足够的知识储备和应变能力。
根据《中华人民共和国广告法》,不得发布广告的药品为
A.人血白蛋白
B.氨茶碱
C.可待图片
D.狂犬疫苗
E.龙胆泻肝九
正确答案
C
解析
禁止发布广告的药品包括:麻醉药品、精神药品、医疗用毒性药品、放射性药品。可待因片属于麻醉药品,故选C。
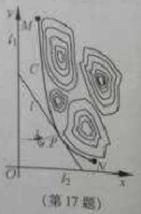
17.某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为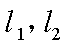
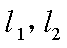
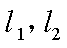
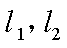
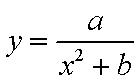
(1)求a,b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式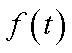
②当t为何值时,公路l的长度最短?求出最短长度.
正确答案
(1)由题意知,点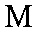
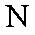
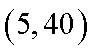
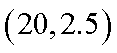
将其分别代入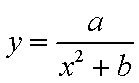
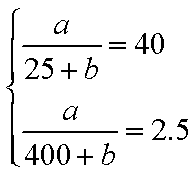
解得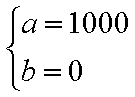
(2)①由(1)知,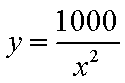

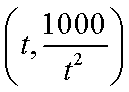
设在点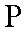
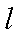
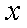
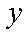
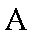
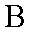
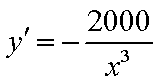
则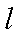
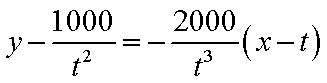
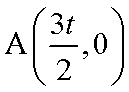
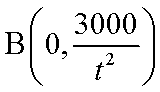
故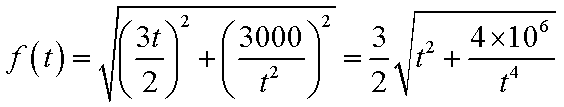
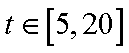
②设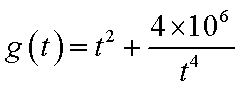
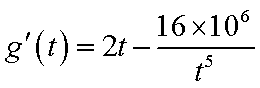
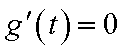
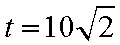
当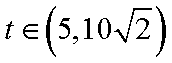
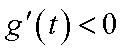
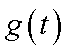
当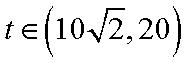
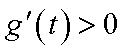
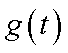
从而,当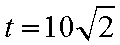
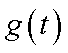
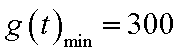
此时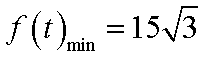
答:当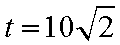
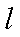
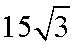
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)试讨论
(2)若


正确答案
(1)



当




当




所以函数



当




所以函数



(2)由(1)知,函数



零点等价于


又




设







从而


此时,
因函数有三个零点,则

所以

解得
综上
解析
解析已在路上飞奔,马上就到!
知识点
15.设曲线

正确答案
(1,1)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析