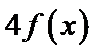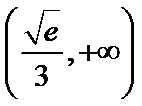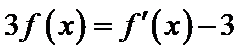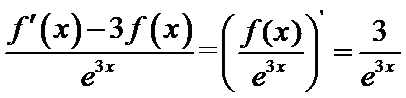- 导数与积分
- 共3028题
10.设函数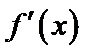

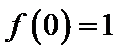
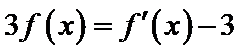
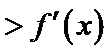
正确答案
解析
:有题意知导函数于原函数之间没有用变量x联系,可知函数与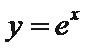
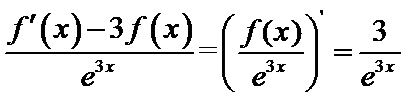
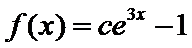
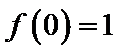
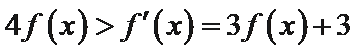
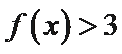
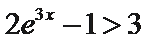

考查方向
解题思路
该题隐含突破点在于
1构造
2根据定积分得原函数函数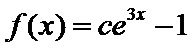
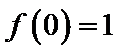
3解指数不等式得出结果
易错点
本题易错于函数的构造过程,
知识点
10.函数

正确答案
解析
考查方向
解题思路
1、根据题意构造函数g(x)=xf(x)再得到函数g(x)的单调区间。
2、根据f(x)奇函数判断出g(x)是偶函数,将不等式进行转化,由图象求出不等式成立时x的取值范围即可。
易错点
1、本题由
知识点
18.已知函数
(Ⅰ)当

(Ⅱ)求证:当



(其中
正确答案
(Ⅰ)函数



(Ⅱ)见解析
解析
(Ⅰ)因为
所以
当

令
得
所以

所以




函数




(Ⅱ)证明:不等式

等价于

即函数

因为
令

因为

当


函数

所以函数


所以不等式

当


所以函数



此时

所以

综上,当



考查方向
本题主要考察了用导数解决函数的单点区间和极值的问题,属于中档题,是高考的热点,解决此类题的关键:
1、(1)确定函数y=f(x)的定义域;
(2)求导数y′=f′(x);
(3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间;
(4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间.
2、当函数f(x)在点x0处连续时,①如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;②如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是极小值。
易错点
1、导数为零的点不一定是极值点 。
2、本题对k的分类讨论不全面导致错误。
知识点
5.已知函数f(x)=
正确答案
解析
由图可知,2个函数图像有3个交点。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查函数图像及零点
解题思路
1、分别画出2个函数图像;
2、求出交点个数,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在画图时发生错误。
知识点
10.已知函数f(x)=x+




f(x1)≥g(x2),则实数a的取值范围是
正确答案
解析
f(x)min=f(1)=5, g(x)min = g(2)=4+a,得a≤1。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查函数的值域
解题思路
1、求出f(x)在[
2、求出f(x)min≥g(x)min,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断范围大小时发生错误。
知识点
21. 设函数f(x)=

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
正确答案
(1)当






解析
⑴解:函数


当



当

当


当


综上:当














































考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
正确答案
知识点
正确答案
知识点
8.正项等比数列{

正确答案
解析

考查方向
本题主要考查极值和数列、对数运算
解题思路
1、求出a1,a4031;
2、求出a2016,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在求a2016时发生错误。
知识点
20.已知函数

(Ⅰ)求函数
(Ⅱ)求证:对于任意


(Ⅲ)试确定曲线

正确答案
(Ⅰ)所以函数

(Ⅲ)当





解析
(Ⅰ)解:函数

求导,得
令

当


所以函数



所以函数

(Ⅱ)证明:假设存在某个


设切点为

所以切线满足斜率

所以
即
所以假设不成立.
所以对于任意


(Ⅲ)解:“曲线


由方程

令



考察函数

因为
所以函数


而方程


所以当



故当





考查方向
解题思路
1、第一问写出函数的定义域,求出导数,然后令导数等于零解方程,列表求极值。
2、第二问直接不易证明,可考虑使用反证法:假设存在某个


3、判断曲线与直线的交点个数问题可以考虑通过函数的极值与直线的相对位置关系以及函数图像的特点采用数形结合的方法判断交点个数;也可以转化为方程判断根的个数进而确定图像交点的个数。由第一问可看出


易错点
第一问中不交待极大值不存在而失分或未考虑函数的定义域而出错;
知识点
扫码查看完整答案与解析