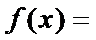- 导数与积分
- 共3028题
设函数
25.讨论函数

26.记


27.在(Ⅱ)中,取


正确答案
(Ⅰ)极小值为
解析
(Ⅰ)



因为

①当

②当

③当







因此,




考查方向
解题思路
(Ⅰ)将



求导得





















易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
解析
:
(Ⅱ)

当

当

由此可知,函数


考查方向
解题思路
当




易错点
绝对值不等式性质运用错误,计算错误,不会合理放缩不等式
正确答案
(Ⅲ)1.
解析
(Ⅲ)



取


由此可知,

考查方向
解题思路
(Ⅲ)当








易错点
平均值不等式的性质,计算能力弱
20.(本小题满分13分)
已知
(I)讨论
(II)当


正确答案
知识点
21.(本小题满分12分)
(I)讨论函数

(II)证明:当



正确答案
知识点
9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是 .
正确答案
7
知识点
(本小题满分12分)
(I)讨论函数

(II)证明:当



正确答案
(Ⅰ)

且仅当



因此当
所以
(II)
由(I)知,
因此,存在唯一


当

当

因此

于是

所以,由
因为

使得

综上,当



知识点
16.已知

的零点个数为___________.
正确答案
0
解析
考查方向
解题思路
易错点
无法从条件中捕捉到有效信息,向结论靠拢。
知识点
(本小题满分13分)
已知函数
(Ⅰ)求函数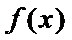
(Ⅱ)当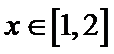
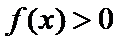
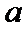
(Ⅲ)试问过点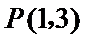
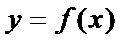
正确答案
考查方向
易错点
1、第一问在对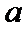
知识点
21.已知函数




(Ⅰ)求

(Ⅱ)证明:当

(Ⅲ)证明:对任意给定的正数



正确答案
(Ⅰ)见解析
(Ⅱ)见解析
(Ⅲ)见解析
解析
(Ⅰ)解,由

因为

所以

令

当



所以当


(Ⅱ)证明,令

由(Ⅰ)得

所以当


(Ⅲ)证明一,①若

由(Ⅱ)知,当



取


②若

要使不等式

而要使


令

所以当


取


又
易知
所以



综上,对任意给定的正数



证明二,对任意给定的正数

由(Ⅱ)知,当


当

因此,对任意给定的正数



证明三,首先证明当

令

由(Ⅱ)知,当

从而


所以

取


因此,对任意给定的正数



考查方向
解题思路
易错点
第一问建议做出极值表便于观察,防止出错;
第二问忽略证明第一问时得到的结论。
知识点
10.已知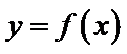
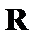
且当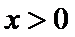
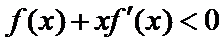
若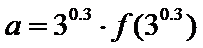
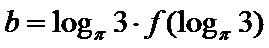
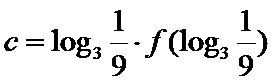
则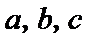
正确答案
解析
试题分析:令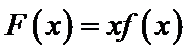
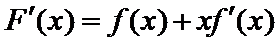
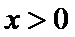
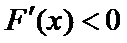
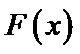
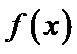
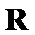
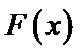
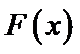
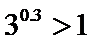
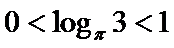
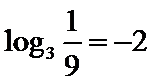
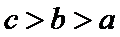
考查方向
解题思路
构造函数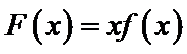
易错点
不能构造出新函数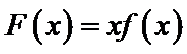
知识点
21.已知函数
(1)若

(2)证明:
正确答案
(1)
(2)见解析.
解析
试题分析:本题属于导数与函数最值的关系、不等式恒成立问题等知识点的综合应用问题,属于拔高题,第二问不容易得分,解析如下:
(1)解:由

即:


在(0,1)上,


所以h(x)在x=1时,取得最大值h(1)=1,即
(2)证明:由(1)知,当k=1时,
令

所以有:


累加得:
考查方向
解题思路
由函数的极值、最值逆求参数的值(或取值范围)问题,往往需要对参数进行分类讨论,如何划分参数讨论的区间成为思维的难点.由于这类问题涉及函数的单调区间,因此分类的标准是使函数在指定的区间内其导数
易错点
相关知识点不熟容易证错。
知识点
扫码查看完整答案与解析