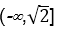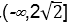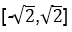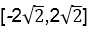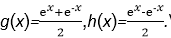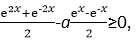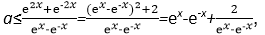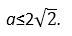导数与积分_章节学习

1

题型：单选题

|

单选题 · 4 分

7．根据下列信息推断，荣誉军人王强伤于（）

A太原会战

B徐州会战

C武汉会战

D百团大战

正确答案

C

解析

此题考查学生对于民国纪年法应用和历史知识的迁移能力。根据材料荣誉军人王强是在民国27年7月在山东临沂受的伤，可以推断时间是1938年7月，正处于武汉、广州会战期间，故正确答案是C项。A项、B项都是1937年，D项是1940年，都应该排除。

考查方向

近代中国的民主革命-抗日战争-武汉会战

解题思路

此题考查学生对于民国纪年法应用和历史知识的迁移能力。根据材料荣誉军人王强是在民国27年7月在山东临沂受的伤，可以推断时间是1938年7月，正处于武汉、广州会战期间，故正确答案是C项。A项、B项都是1937年，D项是1940年，都应该排除。

易错点

本题易错点在于对民国纪年法运算出错而误选。

知识点

变化的快慢与变化率

1

题型：单选题

|

单选题 · 5 分

2.一个物体的运动方程为其中的单位是米，的单位是秒，那么物体在秒末的瞬时速度是（）

A米/秒

B米/秒

C米/秒

D米/秒

正确答案

C

解析

∵物体的运动方程为，

,

故选C.

考查方向

求物体的瞬时速度，只要对位移求导数即可.

解题思路

求出运动方程的导数，据对位移求导即得到物体的瞬时速度，求出导函数在t=3时的值，即为物体在3秒末的瞬时速度

易错点

无

知识点

变化的快慢与变化率

1

题型：单选题

|

单选题 · 5 分

6.已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x)和h(x)分别是R上的偶函数和奇函数,若∀x∈[1,2]使得不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是（）

A

B

C

D

正确答案

B

解析

由F(x)=g(x)+h(x)=ex,

得F(-x)=g(-x)+h(-x)=e-x,

即F(-x)=g(x)-h(x)=e-x,

解得

.∀x∈[1,2],g(2x)-ah(x)≥0恒成立,

即得

分离参数得

因为

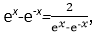
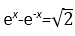
（当且仅当即时取等号,x的解满足[1,2]）

所以

知识点

变化的快慢与变化率

1

题型：单选题

|

单选题 · 5 分

5．为平面内的动点，A、B、C是平面内不共线的三点，满足，则点轨迹必过△的（）

A重心

B外心

C垂心

D内心

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率

1

题型：填空题

|

填空题 · 5 分

12．已知函数f（x）=x3+ax2-2x在区间（-1,+∞）上有极大值和极小值，则实数a的取值范围是______________

正确答案

（-∞,）

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率

1

题型：单选题

|

单选题 · 5 分

6.某几何体的三视图如图所示,则该几何体的体积是（　　）.

A

B3

C

D

正确答案

C

解析

由三视图可知该几何体是一个直三棱柱ABC-A'B'C'截下一个三棱锥B'-A'C'E,其中AA1=AB=BC=2,BE=1,且AB,BC,BE两两垂直,所以多面体ABC-A'EC'的体积V=VABC-A'B'C'-VA'-B'C'E=

知识点

变化的快慢与变化率

1

题型：单选题

|

单选题 · 5 分

7. 如果函数的图像关于点中心对称，那么的最小值为

A

B

C

D

正确答案

C

解析

因为图象关于点中心对称，所以将点的坐标带入函数中，可以得到

φ=kπ-8×的，K是整数，令k=3,可得的最小值为所以选C

考查方向

正弦函数的图象的性质，函数y=Asin（wx+φ）的图象与性质

解题思路

先利用图象关于点对称求出φ的取值集合，然后求出最小值。

易错点

复合三角函数的对称性的应用

知识点

变化的快慢与变化率

1

题型：简答题

|

简答题 · 13 分

设的导数满足其中常数.

（1）求曲线在点处的切线方程。

（2）设求函数的极值。

正确答案

（1）

（2）

解析

（1）因，故，

令，得，由已知，解得

又令，得，由已知，解得

因此，从而

又因为，故曲线在点处的切线方程为，即

（2）由（1）知，，从而有，

令，解得。

当时，，故在为减函数，

当时，，故在为增函数，

当时，，故在为减函数，

从而函数在处取得极小值，在出取得极大值

知识点

导数的几何意义导数的运算

1

题型：简答题

|

简答题 · 13 分

已知函数，．

当时，求曲线在点处的切线方程；

当时，若曲线上的点都在不等式组所表示的

平面区域内，试求的取值范围．

第(1)小题正确答案及相关解析

正确答案

．

解析

当时, ，．

．

则，而．

所以曲线在点(1,)处的切线方程为，即．

…………………………………………………………………………4分

第(2)小题正确答案及相关解析

正确答案

．

解析

依题意当时，曲线上的点都在不等式组所表示的平面区域内，等价于当时，恒成立．

设，．

所以．

（1）当，即时，当时，，为单调减函数，

所以．依题意应有

解得所以．

（2）若，即时，当，，为单调增函

数，

当，，为单调减函数．

由于，所以不合题意．

（3）当，即时，注意到，显然不合题意．

综上所述，． …………………………………………13分

1

题型：简答题

|

简答题 · 13 分

已知函数，．

当时，求曲线在点处的切线方程；

当时，若曲线上的点都在不等式组所表示的

平面区域内，试求的取值范围．

第(1)小题正确答案及相关解析

正确答案

．

解析

当时, ，．

．

则，而．

所以曲线在点(1,)处的切线方程为，即．

…………………………………………………………………………4分

第(2)小题正确答案及相关解析

正确答案

．

解析

依题意当时，曲线上的点都在不等式组所表示的平面区域内，等价于当时，恒成立．

设，．

所以．

（1）当，即时，当时，，为单调减函数，

所以．依题意应有

解得所以．

（2）若，即时，当，，为单调增函

数，

当，，为单调减函数．

由于，所以不合题意．

（3）当，即时，注意到，显然不合题意．

综上所述，． …………………………………………13分

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析