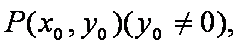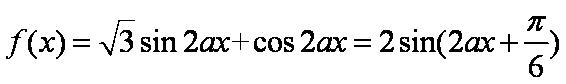- 导数与积分
- 共3028题
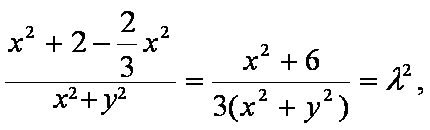
已知函数f(x)=
(1)设f(x)在x0处取得极值,且x0∈(n,n+1),n∈Z,求n的值,并说明x0是极大值点还是极小值点;
(2)求证:f(x0)∈(5,7)
正确答案
见解析
解析
(1)∵ 函数f(x)=
∴ f′(x)=1+



f′(1)=1+

f′(2)=1+




∴ f′(x)=0在(1,2)内有解,
g(x)=x2+
g′(x)=2x+


∴ g(x)在(0,+∞)单调递增,∴g(x)=0,在(0,+∞)只有1解,
∴ f′(x)=0,(0,+∞)只有一解x0,且x0∈(1,2)
即n=1;
又x<x0时,f′(x)<0,x>x0,f′(x)>0
∴ x0为极小值点;
(2)f(x0)=
∵ f′(x)=0,
∴ x02+
得:ln(x0+2)=x02+
∴ f(x0)=



其中x0∈(1,2)中h(x)单调递增
h(1)=






又∵f′(



由二分法知:x0∈(
f(





∴ f(x0)∈(5,7)(14分)
知识点
在四棱锥




(1)当

(2)若



正确答案
见解析
解析
(1)当

又因为


又



为


则
设
要使
所以

由此可知

当且仅当



由此可知

则


取平面
则

因此二面角
知识点
已知椭圆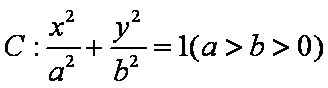

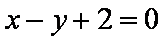
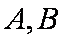


(1)求椭圆的标准方程;
(2)若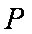
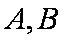
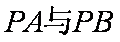
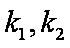
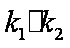
(3)
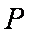
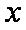
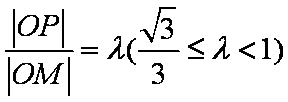
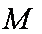
正确答案
见解析。
解析
(1)由题意可得圆的方程为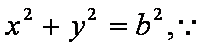
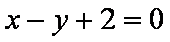
即
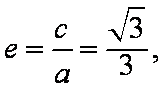
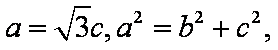
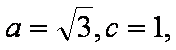
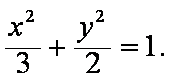
(2)设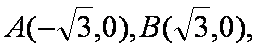
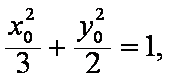
则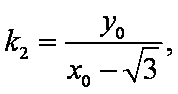
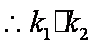
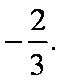
(3)设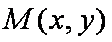
由已知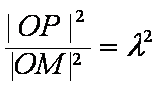
整理得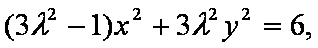
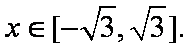
①当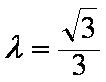
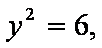
轨迹是两条平行于x轴的线段;
②当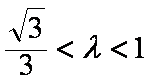
的部分。
知识点
已知



正确答案
解析
本题为几何概率.区域



知识点
已知椭圆
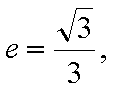
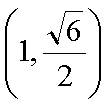
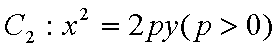
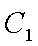
(1)过F的直线与抛物线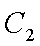
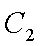
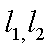
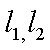
(2)从圆O: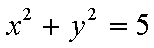
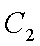
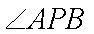
正确答案
见解析
解析
(1)由于椭圆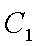
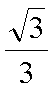
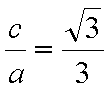
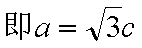
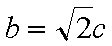
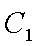
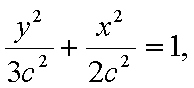
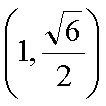
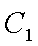
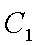
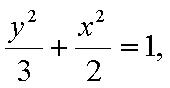
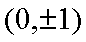
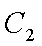
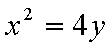
易知直线MN的斜率一定存在,设为k,则直线MN的方程为y=kx+1,代入抛物线的方程得到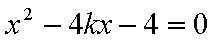
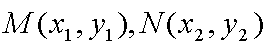
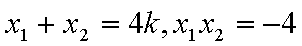
由于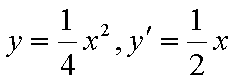
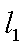
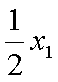
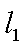
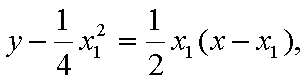
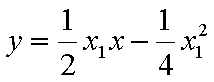
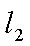
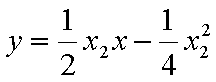

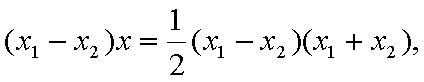
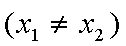

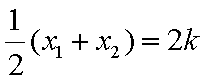
,即点Q(2k,-1),故点Q的轨迹方程是y=-1
(2)当这两条切线中有一条切线的斜率不存在时,根据对称性,不妨设点P在第一象限,则此时点P的横坐标为

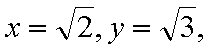
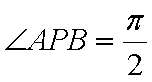
当这两条切线的斜率都存在时,设点P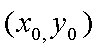

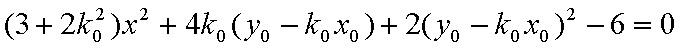
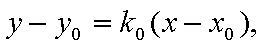
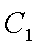
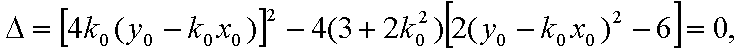
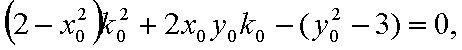
设切线PA,PB的斜率分别为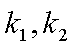
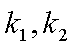
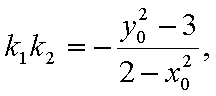
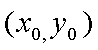
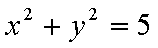
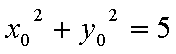
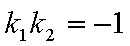
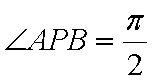
综上可知,角APB的大小为定值,且这个定值为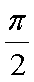
知识点
某几何体的三视图如图所示,且该几何体的体积是
正确答案
解析
由三视图可知,这个几何体是一个底面为直角梯形的四棱锥,底面积为S=


知识点
已知抛物线C的极坐标方程为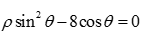
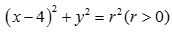
正确答案
解析
将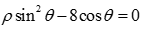
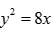
知识点
已知函数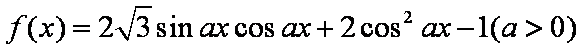
(1)求a的值;
(2)求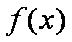
正确答案
见解析。
解析
(1)
令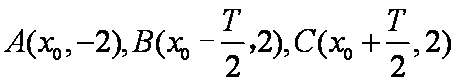
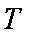
则
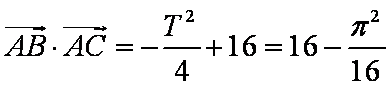
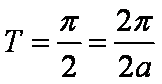
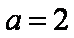
(2)因为
所以
解得
所以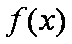
知识点
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出
前






第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数
为60.
(1)请在图中补全频率分布直方图;
(2)若




① 若



成功,且面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为


②若







正确答案
见解析
解析
(1)因为第四组的人数为



(2)设事件
(3)由题意得,



分布列为
知识点
如图,已知

(1)求
(2)若⊙O的半径为







正确答案
见解析。
解析
(1)连接

(2)连接

所以




所以



在

则
知识点
扫码查看完整答案与解析