导数与积分
共3028题

导数与积分
共3028题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

若函数，则=_______________

正确答案

2014

解析

=++++++++

=++++

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

在△ABC中，角A、B、C所对的边分别为a,b，c，已知c=2。acosB－bcosA=。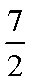

（1）求bcosA的值；

（2）若a=4，求△ABC的面积。

正确答案

见解析

解析

（1）∵，根据余弦定理得，，

∴ ，又∵ ，∴ ，

∴ .

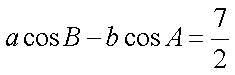
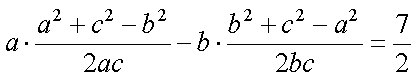
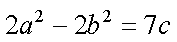
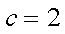
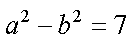
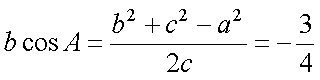
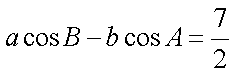
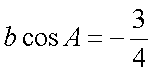
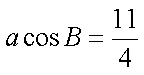
（2）由及，得.

又∵ ，∴ ，∴ ，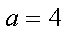

∴ .

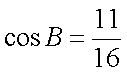
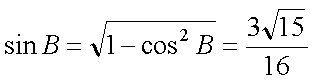
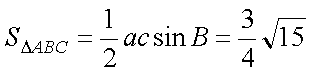
知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知集合，，则等于（）

正确答案

解析

由B得，因此选A

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

已知函数的定义域为R，其导数满足，常数为方程的实数根。

（1）求证：当时，总有成立；

（2）对任意，若满足求证：

正确答案

见解析。

解析

（1）令则

函数为R增函数

当时

当时，总有成立

（2）证明：

又

在是增函数

由（1）知：；

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

已知向量，满足，则向量，夹角的余弦值为（）

正确答案

解析

解析：解法1：，

解法2：数形结合方法

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

某流程图如图所示，现输入如下四个函数，则可以输出的函数是

正确答案

解析

根据程序框图知输出的函数为奇函数，并且此函数存在零点，经验证：不存在零点；不存在零点；为偶函数，且的定义域为全体实数，且，故此函数为奇函数，且令，得，函数存在零点，答案C

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

19.已知函数=。

（1）讨论的单调性；

（2）设，当时，,求的最大值；

（3）已知，估计ln2的近似值（精确到0.001）

正确答案

见解析。

解析

（1）+-2≥0，等号仅当x=0时成立，所以f（x）在（—∞，+∞）单调递增

（2）g（x）=f(2x)-4bf(x)=--4b(-)+(8b-4)x

(x)=2[++]=2(+)(+)

（1）当b2时，g’(x) 0,等号仅当x=0时成立，所以g(x)在(-,+)单调递增，而g(0)=0，所以对任意x>0,g(x)>0;

（2）当b>2时，若x满足，2< <2b-2即 0<x<ln(b-1+)时g’(x)<0,而

g（0）=0,因此当0<Xln(b-1+)时，g(x)<0

综上，b的最大值为2

（3）由（2）知，g(ln)=-2b+2(2b-1)ln2

当b=2时，g(ln)=-4+6ln2>0,ln2>>0.6928

当b=+1时，ln(b-1+)=ln

g(ln)=-2+(3+2)ln2<0

ln2<<0.693

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

如图，在四棱锥中，四边形为平行四边形，为上一点，且.

（1）求证：;

（2）若点为线段的中点，求证：;

（3）若 ,且二面角的大小为,

求三棱锥的体积。

正确答案

见解析。

解析

（1）∵∴

又

（2）

（3）

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

在△ABC中，角A，B，C所对的边分别为，已知函数 R）。

（1）求函数的最小正周期和最大值；

（2）若函数在处取得最大值，求的值。

正确答案

（1）函数的最小正周期是,最大值是

（2）

解析

（1）依题意，

所以函数的最小正周期是,有最大值。

（2）由（I）知：由，得，所以。

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

已知抛物线，过点的直线与抛物线交于、两点，且直线与交于点.

（1）求证: ，、成等比数列；

（2）设，，试问是否为定值，若是，求出此定值；若不是，请说明理由。

正确答案

见解析。

解析

（1）设直线的方程为：，

联立方程可得得: ①

设，，，则， ②

，

而，∴，

即，、成等比数列

（2）由，得，

，

即得：，，则

由（1）中②代入得，

故为定值且定值为

知识点

导数的加法与减法法则

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 导数与积分

扫码查看完整答案与解析