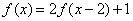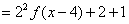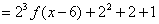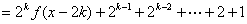- 导数与积分
- 共3028题
已知
(1)记



(2)是否存在a,使函数
正确答案
见解析
解析
知识点
已知函数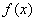
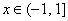
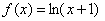
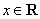
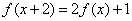
(1)求函数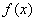
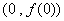
(2)求当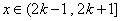
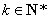
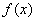
(3)是否存在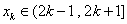
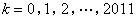

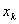

正确答案
见解析。
解析
(1)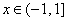
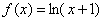
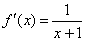
所以,函数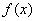
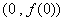
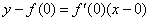
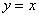
(2)因为
所以,当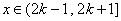
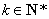
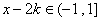
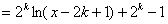
(3)考虑函数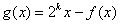
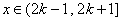
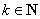
则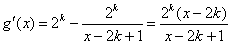
当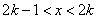
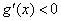
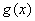
当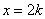
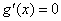
当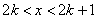
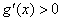
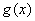
所以,当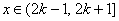
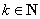
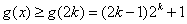
当且仅当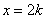
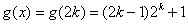
所以,
而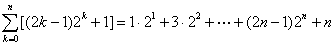
令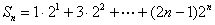
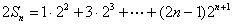
两式相减得,
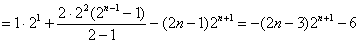
所以,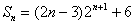
故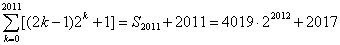
所以,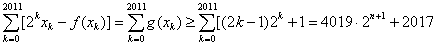
当且仅当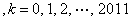
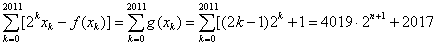
所以,存在唯一一组实数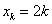
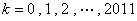
使得等式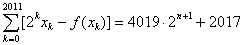
知识点
已知函数

(1)函数



(2)若




(3)当




正确答案
见解析。
解析
(1)∵


∴函数


∵直线



则

(2)当

∴
当




则
∴

(3)不妨设


∵函数



∴
∴

即
等价于
等价于
等价于
∴


知识点
若曲线



正确答案
2
解析
求导得









知识点
已知正数



正确答案
解析
略
知识点
设曲线


的部分有两个交点,则实数
正确答案
见解析
解析


















易知直线

直线

故应有:



知识点
已知函数
①函数

③当



正确答案
解析
略
知识点
直线

正确答案
解析
略
知识点
已知函数


(1)讨论
(2) 若不等式

(3)若方程


正确答案
见解析。
解析
(1)

其导数
①当


②当



所以,

(2)当



能使

当

问题化为求

由于







即

(3)由于



构造函数:

所以函数



于是





知识点
曲线

正确答案
解析
略
知识点
扫码查看完整答案与解析