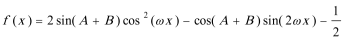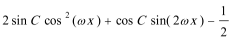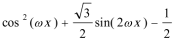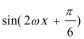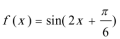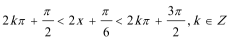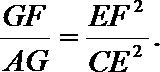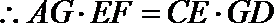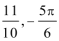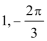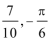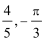- 导数与积分
- 共3028题
17.在△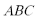
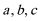
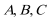
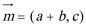
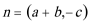
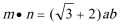
(1)求角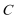
(2)函数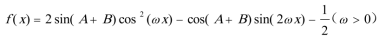
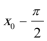
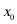
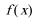
正确答案
(1)因为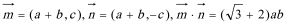
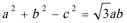
故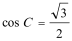
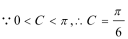
(2)
=
=
=
因为相邻两个极值的横坐标分别为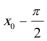
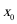
所以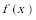
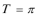
所以
由
所以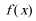
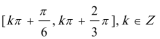
解析
解析已在路上飞奔,马上就到!
知识点
15.将






正确答案
198
解析
解析已在路上飞奔,马上就到!
知识点
16.在锐角






正确答案
b=
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分.
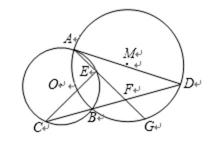
22. 如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD中点,连结AG分别交⊙O、BD于点E、F连结CE.
(1)求证: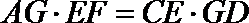
(2)求证:
23. 在直角坐标系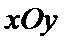
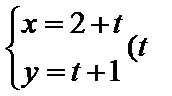

(Ⅰ)求曲线C的普通方程和曲线P的直角坐标方程;
(Ⅱ)设曲线C和曲线P的交点为A、B,求|AB|.
24. 设函数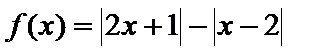
(Ⅰ)求不等式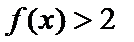
(Ⅱ)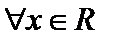
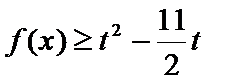
正确答案
22.(1)连结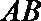
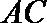
∵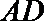
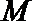
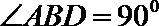
∴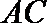
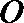
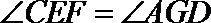
∵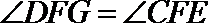
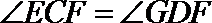
∵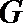
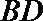
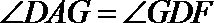
∵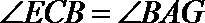
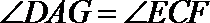
∴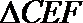
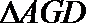
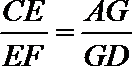
(2)由(1)知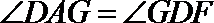
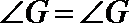
∴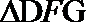
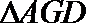
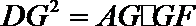
由(1)知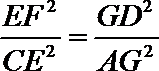
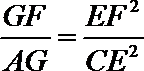
23.(Ⅰ)曲线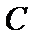
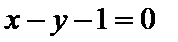
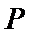
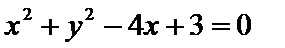
(Ⅱ)曲线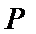
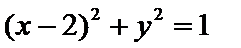
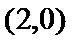
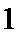
则圆心到直线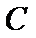
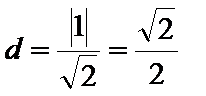
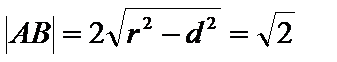
24.
(1)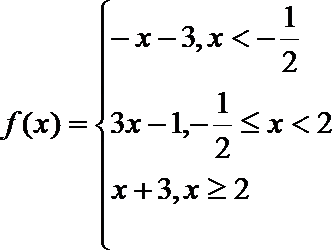
当
当
当
综上所述
(2)易得
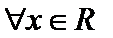
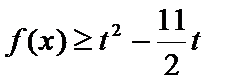
则只需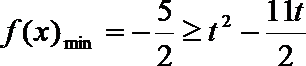
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数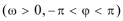
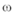
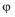
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数




(1)求
(2)设



(3)是否存在实数a,使得当

正确答案
(1)设




故函数
(2)证明:当


因为






又因为



所以当

(3)解:假设存在实数


则
(ⅰ)当





(ⅱ)当





(ⅲ)当






(ⅳ)当






所以
综上可知,存在实数


解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)若



(2)对于给定的负数


求①


正确答案
(1)易知



由题意得 

(2) ① 由


当 



而


因此,
当




综上得

② 当

当

故当且仅当


解析
解析已在路上飞奔,马上就到!
知识点
9. 如图所示,已知正方体






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.口袋里放有大小相等的一个白球和两个红球,有放回地每次摸取一个球,定义数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析