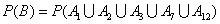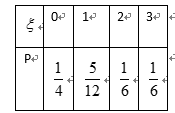- 概率的应用
- 共2题
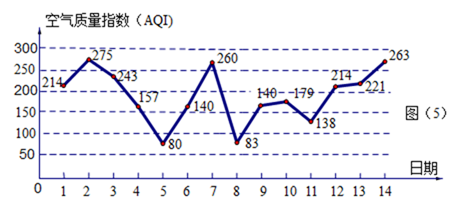
图(5)是某市2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择2月1日至2月12日中的某一天到达该市,并停留3天。
(1)求此人到达当日空气质量重度污染的概率;
(2)设
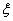
正确答案
见解析。
解析
设
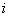

依题意知,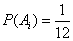
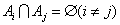
(1)设B为事件“此人到达当日空气质量重度污染”,则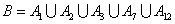
所以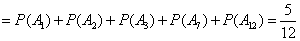
即此人到达当日空气质量重度污染的概率为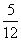
(2)由题意可知,
P(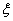

P(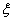
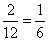
P(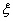

P(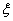

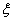
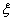
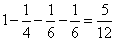
(或P(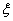
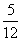
所以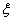
故
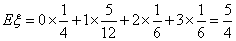
知识点
根据以往的经验,某工程施工期间的将数量X(单位:mm)对工期的影响如下表:
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率。
正确答案
(1)工期延误天数Y的均值为3,方差为9.8
(2)P(Y≤6|X≥300)=
解析
(1)由题意,P(X<300)=0.3,P(300≤X<700)=P(X<700)﹣P(X<300)=0.7﹣0.3=0.4,P(700≤X<900)=P(X<900)﹣P(X<700)=0.9﹣0.7=0.2,P(X≥900)=1﹣0.9=0.1
Y的分布列为
∴E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3
D(Y)=(0﹣3)2×0.3+(2﹣3)2×0.4+(6﹣3)2×0.2+(10﹣3)2×0.1=9.8
∴工期延误天数Y的均值为3,方差为9.8;
(2)P(X≥300)=1﹣P(X<300)=0.7,P(300≤X<900)=P(X<900)﹣P(X<300)=0.9﹣0.3=0.6
由条件概率可得P(Y≤6|X≥300)=
知识点
扫码查看完整答案与解析