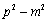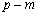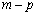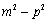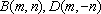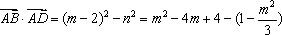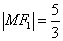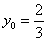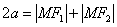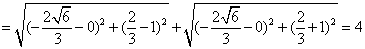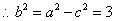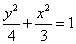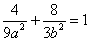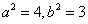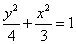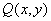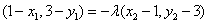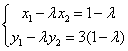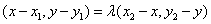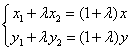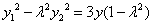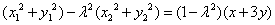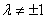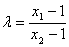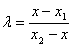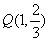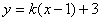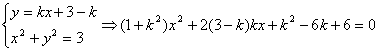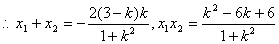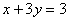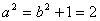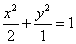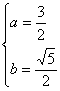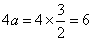- 椭圆及其性质
- 共751题
若椭圆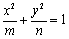
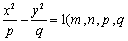
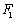
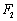
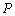
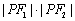
正确答案
解析
由题设可知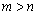
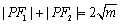
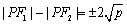
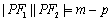
知识点
已知








(1)求椭圆的标准方程。
(2)当

正确答案
见解析。
解析
解析:(1)





(2)


由



设

=
设






知识点
已知椭圆







(1)求椭圆C的方程;
(2)求
(3)直线l交椭圆C于A、B两点,若点A、B的“伴随点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.椭圆C的右顶点为D,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明.
正确答案
见解析
解析
( 1)由已知


(2)当


设


(当且仅当
(3) 设

1)当直线

由

有
由以

整理得: 
将①式代入②式得: 
又点

所以
2) 当直线
联立椭圆方程得: 
代入



综上: 
又

知识点
给定椭圆C: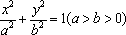
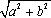
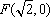
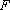
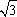
(1)求椭圆C和其“准圆”的方程;
(2)若点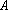

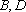
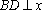
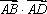
(3)在椭圆C的“准圆”上任取一点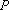
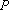
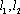
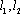
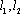
正确答案
见解析
解析
(1)由题意知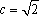
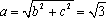
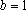
故椭圆C的方程为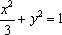
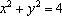
(2)由题意,可设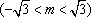
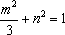
又A点坐标为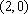
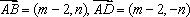
故
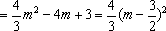

又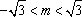
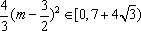
所以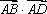
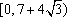
(3)设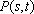
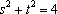
当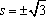
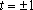
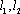
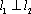
当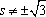
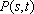
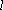
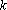
则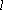
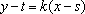
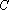
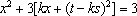
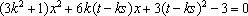
由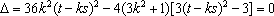
可得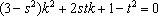
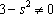
设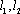
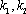
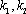
故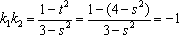
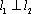
综上可知,对于椭圆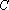
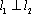
知识点
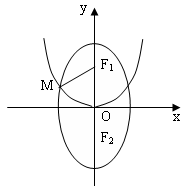
如图,已知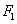
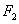
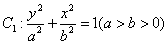
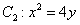
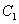
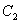
(1)求椭圆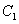
(2)已知点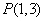
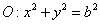
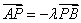
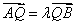
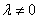
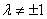
正确答案
见解析。
解析
(1)解法一:令M为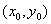
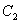
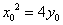
又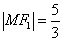
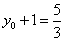
由①②解得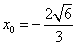
椭圆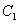
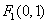
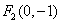
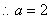
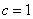

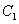
解法二:同上求得M,而点M在椭圆上,故有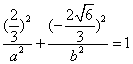
又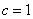
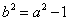

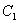
(2)证明:设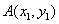
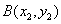
由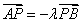
即
由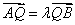
即
⑤×⑦得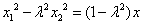
两式相加,得
又点A,B在圆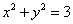
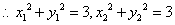
即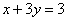
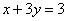
方法二:
由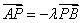
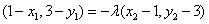
由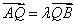
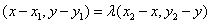
所以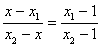
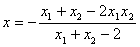
当斜率不存在时,由特殊情况得到
当斜率存在时,设直线为
代入(*)得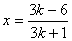
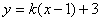
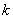
而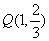
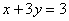
知识点
已知椭圆

(1)若原点到直线

(2)设过椭圆的右焦点且倾斜角为


i)当

ii)对于椭圆上任一点


正确答案
见解析
解析
(1)∵

∵

∵


椭圆的方程为
(2)
i)∵


易知右焦点


由①,②有:
设
∴
ii)显然




设
∵
又点

由③有:
则
……………⑤
又

将⑥,⑤代入④可得:
知识点
已知椭圆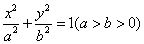
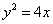
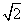
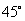
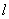
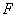
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为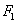
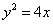
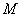
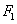
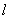
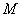
正确答案
见解析。
解析
(1)抛物线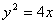
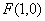
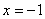
∴ 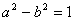
又椭圆截抛物线的准线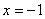
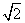
∴ 得上交点为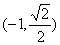
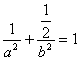
由①代入②得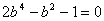
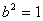
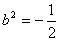
从而
∴该椭圆的方程为该椭圆的方程为
(2)∵ 倾斜角为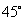
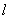
∴ 直线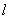
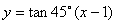
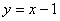
由(1)知椭圆的另一个焦点为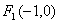
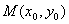
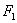
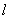
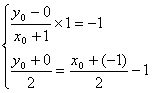
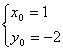
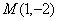
又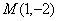
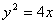
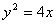
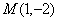
知识点
短轴长为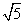
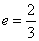
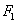
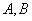
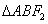
正确答案
6
解析
由题知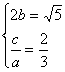
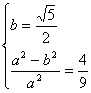
由椭圆的定义知△ABF2的周长为
知识点
已知椭圆C:

(1)求椭圆C的方程;
(2)直线l:y=kx+m(

正确答案
见解析。
解析
(1)由题意

所求椭圆方程为:
(2)联立方程组



设


由点


所以
点


三角形

设



当



当


又
所以当


知识点
已知椭圆





正确答案
解析
略
知识点
扫码查看完整答案与解析