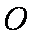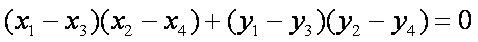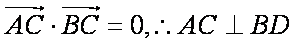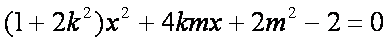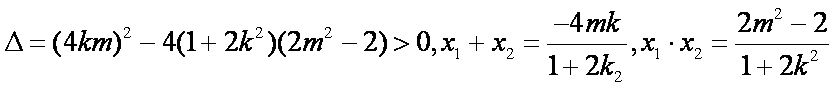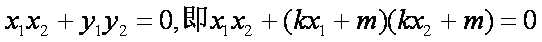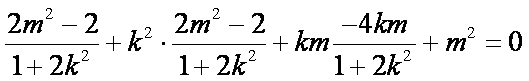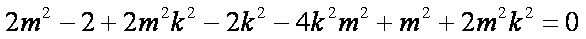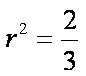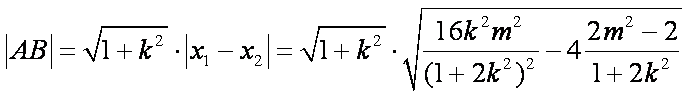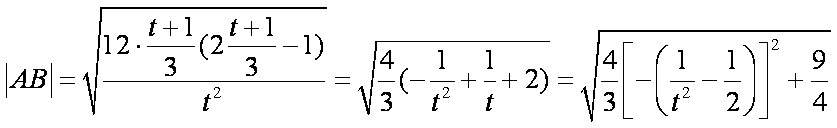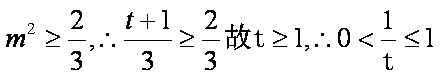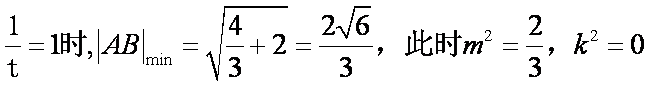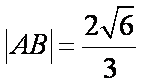- 椭圆及其性质
- 共751题
F1、F2为双曲线C:


正确答案
解析
由










知识点
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC。
正确答案
见解析。
解析
因AE=AC,AB为直径,
故∠OAC=∠OAE。
所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC。
又∠EAC=∠PDE,
所以,∠PDE=∠POC,
知识点
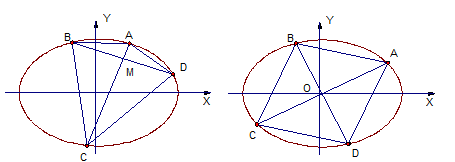
如图,已知椭圆
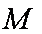
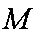
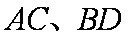
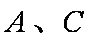
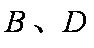
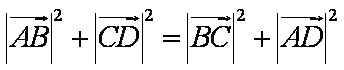
(1)证明:
(2)若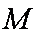
①四边形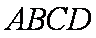
②求弦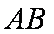
正确答案
见解析
解析
解析:(1)设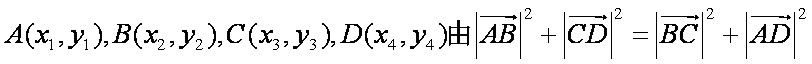
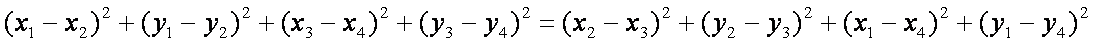
即
∴
即
(2)(i)∵AC⊥BD,由椭圆对称性知AC与BD互相平分,∴四边形ABCD是菱形,它存在内切圆,圆心为O,设半径为r,直线AB方程为:y=kx+m
则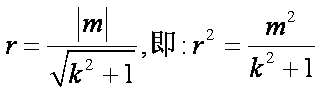
联立 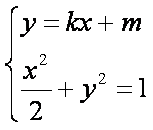
∴
由(1)知OA⊥OB, ∴
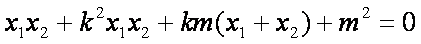
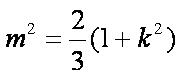
∴存在内切圆,其方程为:
容易验证,当k不存在时,上述结论仍成立.
(ii)
∵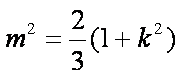
∴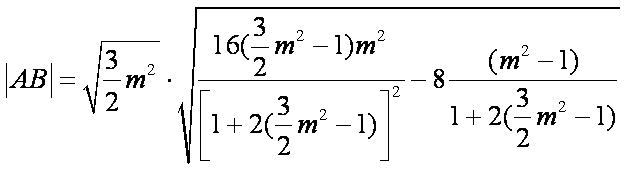
令
∵
当
容易验证,当k不存在时,
知识点
已知椭圆C的中心为原点O,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,当直线l垂直于x轴时,
(1)求椭圆C的方程;
(2)已知点P为椭圆的上顶点,且存在实数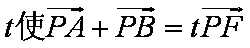
正确答案
见解析。
解析
(1)设椭圆C的方程为: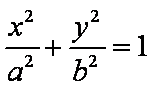
∵当l垂直于x轴时,A,B两点坐标分别是(1,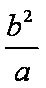
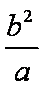
∴ 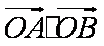
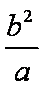
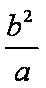
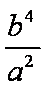
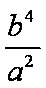
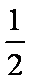
由①,②消去a,得2b4-b2-1=0,∴b2=1或b2=-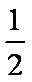
当b2=1时,a2=2 ,因此,椭圆C的方程为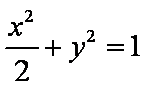
(2)当直线斜率不存在时,易求A(1,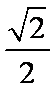
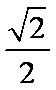
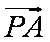
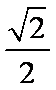
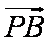
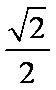
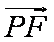
由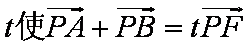
当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
所以,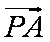
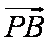
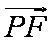
由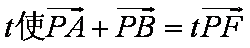
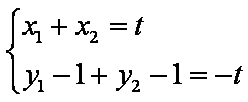
因为y1=k(x1-1),y2=k(x2-1),所以,y1+y2=k(x1+x2-2),解得:k=-1
此时,直线l的方程为y=-x+1,
联立
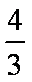
所以,当直线斜率存在时,t=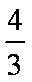
综上所述,存在实数t且t=2时,直线方程为x=1,
当t=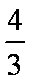
知识点
已知椭圆的焦点坐标为


(1) 求椭圆的方程;
(2) 过

正确答案
见解析。
解析
(1) 设椭圆方程为
由PQ|=3,可得
解得a=2,b=
故椭圆方程为
(2) 设M




则△



因此

由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由

得

则



令t=
则
令f(t)=3t+

当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,
有f(t)≥f(1)=4, 

即当t=1,m=0时,




这时所求内切圆面积的最大值为
故直线l:x=1,△AMN内切圆面积的最大值为
知识点
已知F1,F2是椭圆

正确答案
解析
依题知,F1P⊥F2P,所以,△F1QO∽△F1F2P,
因为△F1OQ与四边形OF2PQ的面积之比为1:2,所以,


则F1P=


e=

知识点
设椭圆C: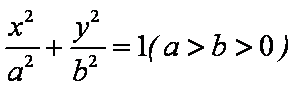
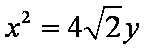
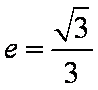
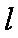
(1)求椭圆C的方程;
(2)是否存在直线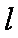
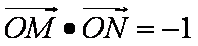
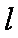
(3)若AB是椭圆C经过原点O的弦,MN∥AB,求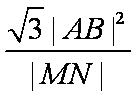
正确答案
见解析。
解析
(1)椭圆的顶点为(0,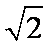
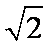
e==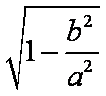
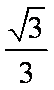
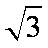
∴椭圆的标准方程为+=1.
(2)由题可知,直线l与椭圆必相交.
①当直线斜率不存在时,经检验不合题意.
②设存在直线l为y=k(x-1)(k≠0),且M(x1,y1),N(x2,y2)。
由得(2+3k2)x2-6k2x+3k2-6=0,
x1+x2=,x1·x2=,
·=x1x2+y1y2=x1x2+k2[x1x2-(x1+x2)+1]
=+k2(-+1)==-1
所以k=±,故直线l的方程为y=(x-1)或y=-(x-1)。
(3)设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(2)可得:|MN|=|x1-x2|=
==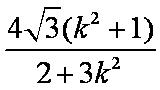
由消去y,并整理得x2=,
|AB|=|x3-x4|=2,
∴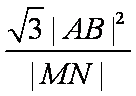
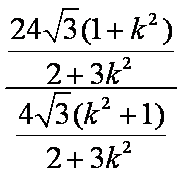
知识点
椭圆




正确答案
解析
因为椭圆的离心率为










知识点
已知椭圆的焦点坐标为


(1) 求椭圆的方程;
(2) 过

正确答案
见解析。
解析
(1) 设椭圆方程为
由PQ|=3,可得
解得a=2,b=
故椭圆方程为
(2) 设M




则△



因此

由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由

得

则



令t=
则
令f(t)=3t+

当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,
有f(t)≥f(1)=4, 

即当t=1,m=0时,




这时所求内切圆面积的最大值为
故直线l:x=1,△AMN内切圆面积的最大值为
知识点
已知直线



(1) 求椭圆
(2) 过点











正确答案
见解析。
解析
(1)则由题设可知
又
所以椭圆C的方程是
(2)解法一:假设存在点T(u, v). 若直线l的斜率存在,设其方程为
将它代入椭圆方程,并整理,得
设点A、B的坐标分别为
因为
所以
当且仅当
所以
此时以AB为直径的圆恒过定点T(0,1).
当直线l的斜率不存在,l与y轴重合,以AB为直径的圆为
综上可知,在坐标平面上存在一个定点T(0,1),满足条件.
解法二:若直线l与y轴重合,则以AB为直径的圆是
若直线l垂直于y轴,则以AB为直径的圆是
由

由此可知所求点T如果存在,只能是(0,1).
事实上点T(0,1)就是所求的点. 证明如下:
当直线l的斜率不存在,即直线l与y轴重合时,以AB为直径的圆为
当直线l的斜率存在,设直线方程为

设点A、B的坐标为
因为
所以
综上可知,在坐标平面上存在一个定点T(0,1)满足条件.
知识点
扫码查看完整答案与解析