- 椭圆及其性质
- 共751题
已知椭圆

(1)求椭圆C的方程;
(2)设直线
求证:直线
正确答案
见解析
解析
解析:
(1)由椭圆C的离心率


椭圆C的左、右焦点分别为
解得

(2)由题意,知直线MN存在斜率,其方程为
消去
△=(4km)2—4(2k2+1)(2m2—2)>0
设

且
由已知直线F2M与F2N的倾斜角互补,得
化简,得
整理得
直线MN的方程为
因此直线MN过定点,该定点的坐标为(2,0)
知识点
已知在直角坐标系






(1)以原点为极点、



(2)在(1)的条件下,设直线



正确答案
见解析
解析
解析:(1)圆锥曲线


所以普通方程为




(2)

知识点
已知椭圆






(1)求椭圆
(2)过椭圆左焦点





正确答案
见解析。
解析
(1)



∴椭圆E的方程为:
(2)设点

由方程组


由已知得:
知识点
已知椭圆



(1)求椭圆的离心率
(2) 直线AB的斜率;
(3)设点C与点A关于坐标原点对称,直线



正确答案
(1)

解析
解析: (1)解:由




(2)解:由(1)知,
设直线AB的方程为
由已知设
消去y整理,得
依题意,
而
联立三式,解得

(3)由(2)知,


线段



直线





当

知识点
如图所示,在



(1)求点M的轨迹方程;
(2)过点




正确答案
(1)

(2)12
解析
(1)设




∴


(2)设



直线



由

则
∵


∴
知识点
已知椭圆





(1)求
(2)设斜率不为









正确答案
见解析
解析
解析:(1)设
和

且




(2)设直线






设切点







化简并整理得


知识点
已知椭圆椭圆








(1)求椭圆
(2)点








正确答案
见解析
解析
(1)


准圆方程为
(2)(1)因为准圆


设过点

所以由


因为椭圆与
所以

所以

①当

因为

当



此时经过点



即



同理可证


②当


设经过点

则


由
因为

设


所以

所以

综合①②知:因为



所以线段


知识点
如图,已知









(1)当




(2)已知直线












正确答案
见解析
解析
(1)由题意知,直线

又



∵





∵




即

∴直线


(2)由题意易得,线段

∵直线

∴直线

又∵


∴直线

将直线


易知方程①的判别式
方程②的判别式
由(1)易知



设

∴线段


又∵
∴线段


∴





∵


∴



∴


故椭圆

知识点
设椭圆






(1)当
(i)若椭圆


(ii)当点P在直线


(2) 当



正确答案
见解析
解析
(1)(i) 





(ii)设




将直线


则直线F1P的斜率



故直线F2P的方程为y=

即点Q坐标为


所以

所以F1P⊥F1Q, -----------10分
(2)点P过定直线,方程为
知识点
已知椭圆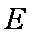
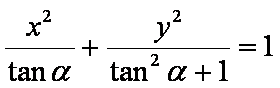
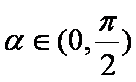
(1)求椭圆
(2)若椭圆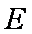
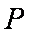
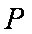
正确答案
见解析。
解析
(1)根据已知条件有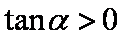
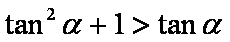
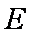
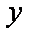
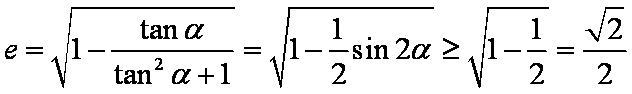
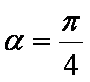
由于椭圆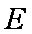
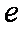
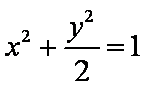
(2)设交点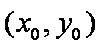
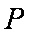
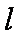
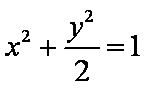
(i)当斜率不存在或等于零时,易得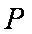
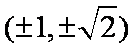
(ii)当斜率存在且非零时,则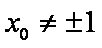
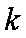
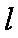
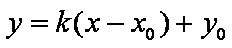
与椭圆方程联立消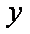
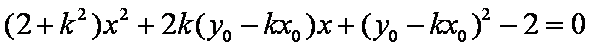
由相切,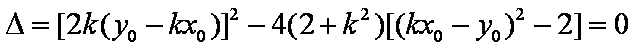
化简整理得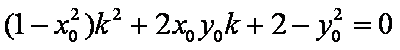
因过椭圆外一点有两条直线与椭圆相切,由已知两切线垂直,故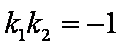
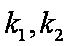
故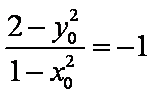

又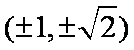
故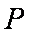
知识点
扫码查看完整答案与解析