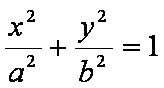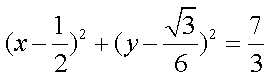- 椭圆及其性质
- 共751题
如图,已知椭圆E:


(1)求椭圆E的方程以及点Q的坐标;
(2)过点Q的动直线l交椭圆E于A、B两点,连结AF并延长交椭圆于点C,连结
正确答案
解析
(1)设点F(c,0),Q(x,0)(
由
可得

依题意 

又因为

故椭圆的方程是
(2)① 设直线l的方程为
依题意, 

此时,若设


点B关于x轴的对称点B1(
由(*)可知上述关系成立。
因此,点C即是点B1,这说明B、C关于x轴对称
② 由① 得B、C关于x轴对称,同理,A、D关于x轴对称。
所以,四边形ABCD是一个等腰梯形,则四边形ABCD的面积

设


求导可得


由于


所以,当

四边形ABCD的面积S取得最大值,
此时,直线l的方程是
知识点
已知椭圆C:



(1)求椭圆C的方程;
(2) 在x轴上是否存在一定点E,使得对椭圆C的任意一条过E的弦AB,
为定值?若存在,求出定点和定值;若不存在,请说明理由。
正确答案
见解析。
解析
(1)设椭圆C的方程为





由①②得:


(2)设

则
解得

下证





则



综上得定点为E

知识点
已知椭圆
(1)求椭圆的方程;
(2)若C、D分别是椭圆长轴的左、右端点,动点M
满足
证明
(3)在(2)的条件下,试问在x轴上是否存在异于点C的定点Q,使以线段MP为直径的圆恒过直线DP、MQ的交点,若存在,求出Q的坐标,若不存在,说明理由。
正确答案
见解析。
解析
(1)如图,由题知

(2)C(-2,0),D(2,0),则可设

(3)设


知识点
已知椭圆







(1)求椭圆
(2)求
(3)若



正确答案
见解析。
解析
(1)易知



故方程为
(2)证明:设





设

∴
=


故所求范围是
(3)由对称性可知N

直线AN:


∴直线

知识点
已知直线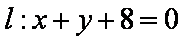
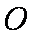
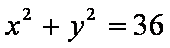
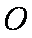

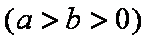
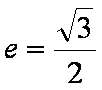
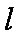
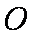
(1)求椭圆
(2)过点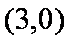
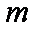

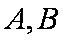
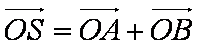
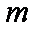
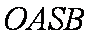
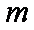
正确答案
见解析。
解析
(1)∵圆心O到直线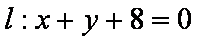
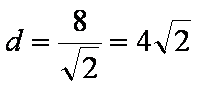
直线l被圆O截得的弦长2a=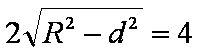
又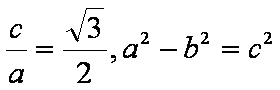
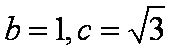
∴椭圆C的方程为:
(2)∵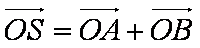
假设存在这样的直线l,使四边形OASB的对角线长相等,
则四边形OASB为矩形,因此有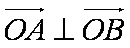
设A(x1,y2),B(x2,y2),则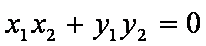
直线l的斜率显然存在,设过点(3,0)的直线l方程为: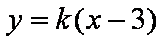
由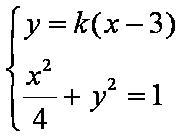
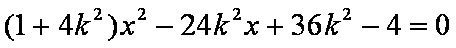
由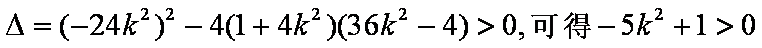
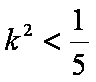
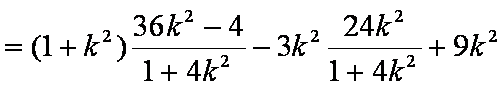
由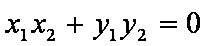
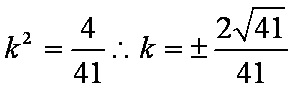
故存在这样的直线l,其方程为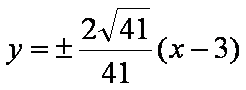
知识点
已知椭圆



(1)求椭圆
(2)设椭圆












(3)当P不在



正确答案
见解析
解析
(1)∵
∵直线
∴
∵椭圆C1的方程是
(2)∵MP=MF2,
∴动点M到定直线
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线
∴点M的轨迹C2的方程为 
(3)显然











若存在C、D关于




设线段








将









∵










所以在曲线

知识点
已知椭圆






(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为






正确答案
见解析
解析
解:(1)抛物线


∴ 
又椭圆截抛物线的准线

∴ 得上交点为

由①代入②得


从而
∴ 该椭圆的方程为该椭圆的方程为
(2)∵ 倾斜角为


∴ 直线

由(1)知椭圆的另一个焦点为




解得

又







知识点
已知椭圆C的中心在原点,一个焦点的坐标为F(

(1)求椭圆C的方程;
(2)直线y=x-1与椭圆C交于A、B两点,求弦长|AB|; (3)设P是椭圆C上的任意一点,MN是圆D:x2+(y-3)2=1的任意一条直径,求
正确答案
见解析。
解析
(1)设椭圆方程为



∴椭圆的方程为
(2)由




(3)设P(x0,y0),则
=
=-(
∵y0∈[-


知识点
如图,设圆弧









正确答案
解析
由图像和三角形相关知识得到当所围三角形为等腰直角三角形,当切点A为等腰直角三角形斜边中点时概率P最大.可求的此时等腰三角形边长为


知识点
已知椭圆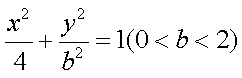
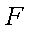
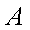
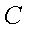
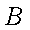
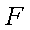
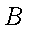
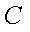
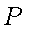
(1)当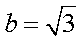
(2)直线AB与圆P能否相切?证明你的结论.
正确答案
见解析。
解析
(1)设F、B、C的坐标分别为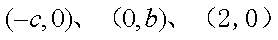
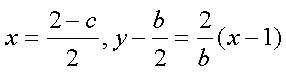
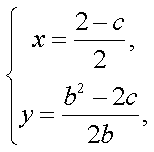
所以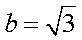
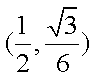
圆P方程为
(2)直线AB与圆P不能相切.
理由如下:
因为
如果直线AB与圆P相切,则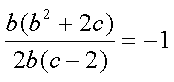
解得c=0或4,
又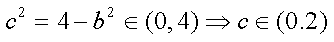
而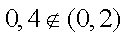
知识点
扫码查看完整答案与解析