- 椭圆及其性质
- 共751题
18. 已知点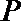
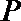
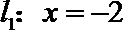
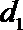
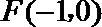
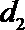
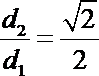
(1)求动点P所在曲线C的方程;
(2)直线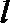
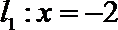
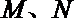
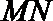
(3)记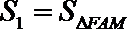
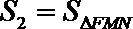
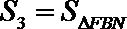
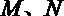
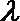
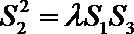
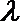
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知椭圆C:


(1)求椭圆C的方程;
(2)过原点且斜率为
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知椭圆C:
(1)若P(-1,
(2)是否存在这样的椭圆C,使得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 椭圆



(1)求椭圆
(2)若





(3)设圆Q:







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆


(I)求椭圆C的方程;
(II)若椭圆C上两点M,N使
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 在平面直角坐标系xOy中,椭圆C:

(1)求a,b的值。
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点。
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,椭圆C1: 


(I)求C1,C2的方程.
(II)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E. 求
正确答案
(Ⅰ)由题意知e==,从而a=2b.
又2=a,所以a=2,b=1.
故C1,C2的方程分别为+y2=1,y=x2-1.
(Ⅱ)证明:由题意知,直线l的斜率存在
设为k,则直线l的方程为y=kx.
由得x2-kx-1=0.
设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根
于是x1+x2=k,x1x2=-1.
又点M的坐标为(0,-1),
所以kMA·kMB=
故MA⊥MB,即MD⊥ME,故
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知椭圆







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 如图,正方形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





















