• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 椭圆及其性质
  • 共751题
  • 椭圆及其性质
  • 共751题

热门试卷

X 查看更多试卷
1
题型： 单选题
|
单选题 · 5 分

7．与椭圆有公共焦点，且离心率互为倒数的双曲线的方程是（     ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质双曲线的定义及标准方程
1
题型：简答题
|
简答题 · 14 分

20．已知之间满足 。

（1）方程表示的曲线经过一点，求b的值；

（2）动点(x,y)在曲线(b>0)上变化，求x22 y的最大值；

（3）由能否确定一个函数关系式，如能，求解析式；如不能，再加什么条件就可使之间建立函数关系，并求出解析式。

正确答案

（1） ,

（2）根据得

,

,

, 

（3）不能,如再加条件就可使之间建立函数关系,

解析式  （不唯一，也可其它答案）

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程椭圆的几何性质
1
题型：简答题
|
简答题 · 13 分

20.已知以原点O为中心的椭圆，它的短轴长为，右焦点(c>0)，它的长轴长为2a(a>c>0)，直线与x轴相交于点A，，过点A的直线与椭圆相交于P.Q两点。

（Ⅰ）求椭圆的方程和离心率；

（Ⅱ）若，求直线PQ的方程；

（Ⅲ）设，过点P且平行于直线的直线与椭圆相交于另一点M，证明：。

正确答案

(Ⅰ)解：由题意，可知椭圆的方程为.

由已知得

解得，c=2，

所以椭圆的方程为，离心率.

(Ⅱ)解：由（1）可得A(3，0)．设直线PQ的方程为y=k(x－3).

联立方程组，得(3k2+1)x2－18k2x+27k2－6=0，

依题意△=12(2－3k2)>0，得.

设P(x1，y1)，Q(x2，y2)，则

，  ①     

．  ②

由直线PQ的方程得为y1=k(x1－3)，y2=k(x2－3)，于是，

y1y2=k2(x1－3) (x2－3)= k2[x1x2－3(x1+ x2)+9].        ③

∵，∴x1x2+y1y2=0．    ④

由①②③④得5k2=1，从而．

所以直线PQ的方程为或．

(理科做)

(Ⅲ)证明：∵P(x1，y1)，Q(x2，y2)， A(3，0)，

∴，．由已知得方程组

，注意λ>1，解得，

因为F(2，0)， M(x1，－y1)，故

.

而，所以.

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系椭圆的定义及标准方程椭圆的几何性质直线、圆及圆锥曲线的交汇问题
1
题型：填空题
|
填空题 · 5 分

7．对于椭圆，定义为椭圆的离心率，椭圆离心率的取值范围是，离心率越大椭圆越“扁”，离心率越小则椭圆越“圆”。若两椭圆的离心率相等，我们称两椭圆相似。已知椭圆与椭圆相似，则的值为_________

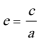
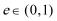
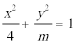
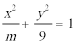
正确答案

6

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质
1
题型： 单选题
|
单选题 · 5 分

9．已知有相同两焦点F1、F2的椭圆 + y2=1（m>1）和双曲线 - y2=1（n>0），P是它们的一个交点，则ΔF1PF2的形状是（    ）

A锐角三角形

B直角三角形

C钝有三角形

D随m、n变化而变化

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质双曲线的几何性质
1
题型：填空题
|
填空题 · 5 分

16．以下四个关于圆锥曲线的命题中：

①设A、B为两个定点，k为非零常数，，则动点P的轨迹为双曲线；

②过定圆C上一定点A作圆的动点弦AB，O为坐标原点，若则动点P的轨迹为椭圆；

③方程的两根可分别作为椭圆和双曲线的离心率；

④双曲线和椭圆有相同的焦点

其中真命题的序号为_____________（写出所有真命题的序号）

正确答案

③

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用椭圆的定义及标准方程椭圆的几何性质双曲线的定义及标准方程双曲线的几何性质
1
题型：简答题
|
简答题 · 12 分

20．设椭圆的左、右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点．

（1）若直线AP与BP的斜率之积为,求椭圆的离心率;

（2）若|AP|=|OA|,证明直线OP的斜率k满足．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质直线与椭圆的位置关系圆锥曲线中的范围、最值问题
1
题型：填空题
|
填空题 · 5 分

10．已知椭圆和圆,若上存在点,使得过点引圆的两条切线,切点分别为,满足,则椭圆的离心率的取值范围是（    ）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

6.已知直线x=t与椭圆 + =1交于P,Q两点.若点F为该椭圆的左焦点,则使 · 取得最小值时t的值为（       ）

A

B

C

D

正确答案

B

解析

知椭圆的左焦点F(-4,0).

根据对称性可设P(t,y0),Q(t,-y0),

则

所以

又因为

所以

故当时, ·

取得最小值.

知识点

椭圆的几何性质直线与椭圆的位置关系
1
题型： 单选题
|
单选题 · 5 分

8． 椭圆的两焦点分别是，等边的边与该椭圆分别相交于两点，且，则该椭圆的离心率为（     ）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质
继续学习 学习下一知识点
下一知识点 : 双曲线及其性质
百度题库 > 高考 > 理科数学 > 椭圆及其性质

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题