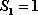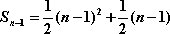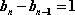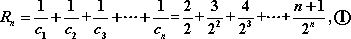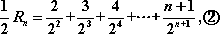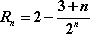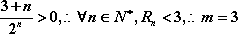- 数列的概念与简单表示法
- 共705题
由等式









(1)试求数列

(2)若甲数列的每一项都是乙数列的项,且乙数列中至少有一项不是甲数列的项,则称甲数列是乙数列的真子数列.试证明:数列

正确答案
见解析
解析
(1)解:由


由

(2)即对任意的



这表明对任意的




而对于










知识点
已知矩阵

(3,1)变为点(1,1),求实数a,k的值。
正确答案
见解析。
解析
设特征向量为
则 
因为k≠0,所以a=2.
因为


所以2+k=3,解得 k=1。
综上,a=2,k=1.
知识点
如图,












(1)写出





(2)求证:

(3)设



正确答案
见解析
解析
(1)依题意,有

(2)证明:①当

②假设当

则当

得
即
解得

即当
综上所述,对所有

(3)

因为函数






由题意,有
所以,
知识点
数列{an}是公差不为0的等差数列,且a1,a3,a7为等比数列{bn}的连续三项,则数列{bn}的公比为( )
正确答案
解析
设数列{an}的公差为d(d≠0),由a32=a1a7得(a1+2d)2=a1(a1+6d)⇒a1=2d,
故
故选 C。
知识点
已知数列{an}是等差数列,a3=5,a5=9.数列{bn}的前n项和为Sn,且
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an•bn,求数列{cn}的前n项和 Tn。
正确答案
见解析。
解析
(1)法一:设数列的公差为d
由题意可得
解得a1=1,d=2
∴an=1+2(n﹣1)=2n﹣1
法二:设数列的公差是d
∴
∴an=a5+2(n﹣5)=9+2n﹣10=2n﹣1
∵
当n=1时,
∴b1=
当n≥2时,bn=sn﹣sn﹣1=
=
∴
∴数列{bn}是以

∴bn=
(2)cn=an•bn=
∴


两式相减可得,
=
=
知识点
已知数列


(1)求常数

(2)若抽去数列



(3) 在(2)的条件下,试求数列


正确答案
见解析
解析
(1)解:由


又因为存在常数

则


故数列

此时


(2)解:由等比数列的性质得:
(i)当

(ii) 当

所以
(3)解:注意到





(i)当

(ii)当

即
知识点
数列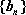
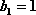

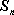

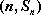
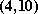
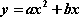
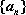
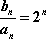
(1)求证:数列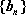
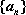
(2)令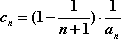
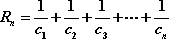
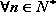

正确答案
见解析。
解析
(1)证明:∵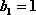
∴点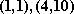
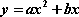
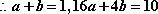
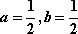
∴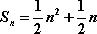
则
∴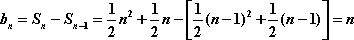
又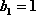
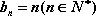
∴数列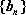
又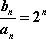
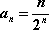
(2)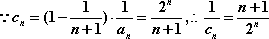
∴
∴
两式相减,得:
∵
知识点
已知等比数列

(1) 求通项
(2) 若




正确答案
见解析。
解析
(1)

于是
(2)由
又因为
所以数列


于是
因为

解得
经过估算,得到
知识点
已知等差数列






(1)求数列
(2)记

(3)求数列


正确答案
见解析
解析
(1)因为






又当


当


所以数列


所以
(2)由(1)知
所以
所以
(3)因为
则

由①-②,得
整理,得
知识点
记

…
可以推测
正确答案
解析
本题考查归纳推理问题.根据各式的规律,显然




知识点
扫码查看完整答案与解析