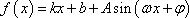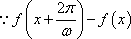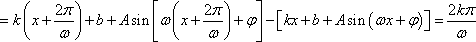- 分段函数的解析式求法及其图象的作法
- 共37题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
定义区间





(1)已知函数



(2)已知函数







(3)定义函数



正确答案
(1)


解析
(1)
解得



画图可得:区间

最小值为
(2)
当

当

所以
所以值域区间长度总和为
(3)由于当


取

所以方程

考虑函数





对于集


取


又因为函数

所以方程

依次记这

从而不等式


对




又有
对比②③中

可得:
知识点
设










正确答案
解析
略
知识点
已知函数f(x)= 
正确答案
解析
f(0)=2,f(f(0))=f(2)=4+2a=4a,所以a=2
知识点
记


正确答案
解析
由向量运算的平行四边形法可知




(或
知识点
若直角坐标平面内的两不同点












正确答案
解析
根据题意可知只须作出函数

知识点
定义:对于函数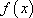
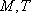
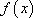

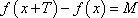
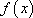
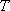
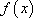
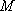
(1)证明函数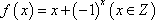
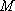
(2)试求一个函数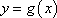
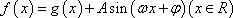
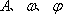
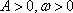
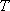
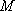
(3)设函数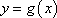
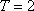
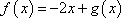
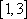
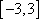
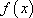
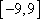
正确答案
见解析
解析
(1)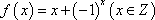
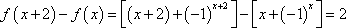
所以函数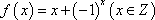
(2)设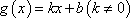
(非零常数) 所以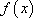
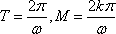
(3)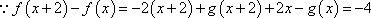
所以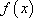
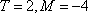
设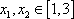
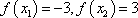
由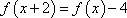
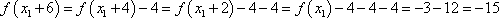
又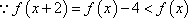
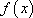
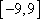

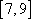
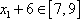
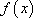
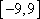
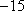
由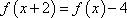
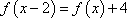
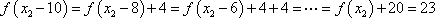
又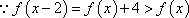
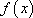
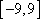

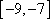
而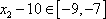
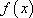
知识点
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元,根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示,经销商为下一个销售季度购进了130 t该农产品,以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润。
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望。
正确答案
(1) 
解析
(1)当X∈[100,130)时,T=500X-300(130-X)=800X-39 000,
当X∈[130,150]时,T=500×130=65 000.
所以
(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
所以ET=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59 400
知识点
已知函数f(x)=x﹣[x],其中[x]表示不超过实数x的最大整数,若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是( )
正确答案
解析
函数f(x)=x﹣[x]的图象如下图所示:
y=kx+k表示恒过A(﹣1,0)点斜率为k的直线
若方程f(x)=kx+k有3个相异的实根。
则函数f(x)=x﹣[x]与函数f(x)=kx+k的图象有且仅有3个交点
由图可得:
当y=kx+k过(2,1)点时,k=
当y=kx+k过(3,1)点时,k=
当y=kx+k过(﹣2,﹣1)点时,k=﹣1,
当y=kx+k过(﹣3,﹣1)点时,k=﹣
则实数k满足 


知识点
12.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析