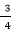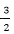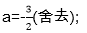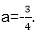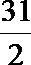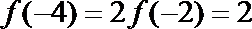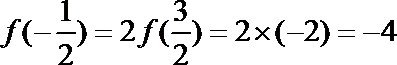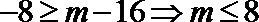- 分段函数的解析式求法及其图象的作法
- 共37题
11.函数

正确答案
解析
考查方向
解题思路
1、对每一段单独求解,但是要在取值范围以内
2、对解集取并集
易错点
本题易错于忽视前提条件
知识点
12.已知函数
则
正确答案
-20
解析

所以

考查方向
解题思路
1) 把

2)代入第二段求值的通项公式;
易错点
本题易把

知识点
10.已知函数
正确答案
0;
解析
试题分析:利用分段函数的解析式求出函数值和函数的最小值。
∵
当x≥1时,

当x<1时,f(x)≥0,当且仅当x=0时取得最小值,所以函数的最小值为
考查方向
解题思路
根据分段函数的解析式,首先求出f(-3)的值为,再求出f(f(-3))的值;分别求
出函数在两段上的最小值,比较得出函数的最小值。
易错点
分段函数求值要代入到对应的解析式中,注意基本不等式等号成立的条件。
知识点
3.已知实数a≠0,函数
正确答案
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
3.已知实数a≠0,函数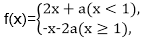
正确答案
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
8.定义在R上的函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,
















(1)求

(2)已知警员的对讲机的有效通话距离是





正确答案
(1)
(2)

解析
(2)甲到达






当

当

所以
因为









知识点
13.已知函数


正确答案
-4
解析
解析已在路上飞奔,马上就到!
易错点
本题易在理解分段函数性质时发生错误,导致题目无法进行。
知识点
王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的130网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍,若要用联通130应最少打多长时间的长途电话才合算. ( )
正确答案
解析
由已知,王先生每月拨打本地电话的时间是拨打长途电话时间的5倍和条件,可知要用联通130应最少打400秒时间的长途电话才合算.
考查方向
本题主要考查分段函数以及资源最优化问题
易错点
少算了甲的费用
知识点
12.定义在 R 上的函数 f (x)满足 f (x + 2) = 


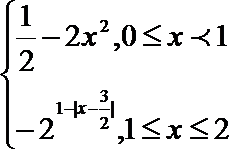
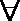
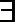
正确答案
解析
∵当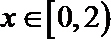

∴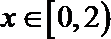

∵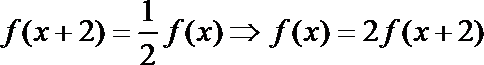
∵当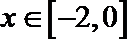
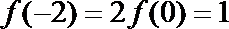
∵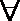
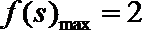
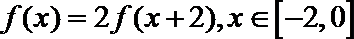
∵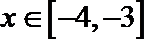

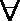
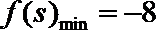
∵函数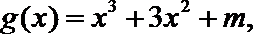
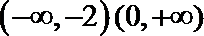
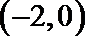
∴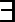

考查方向
本题主要考查函数与不等式综合应用
解题思路
由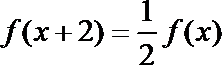
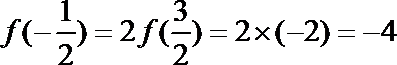
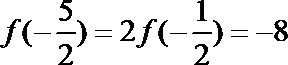
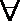
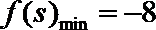
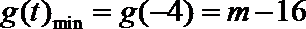
易错点
分段函数如何转化求出最值
知识点
扫码查看完整答案与解析