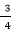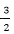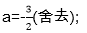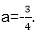- 分段函数的解析式求法及其图象的作法
- 共37题
1
题型:
单选题
|
3.已知实数a≠0,函数
正确答案
A
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
分段函数的解析式求法及其图象的作法奇偶函数图象的对称性
1
题型:
单选题
|
3.已知实数a≠0,函数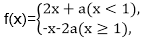
正确答案
A
解析
当a>0时,2-2a+a=-1-a-2a,
解得
当a<0时,-1+a-2a=2+2a+a,
解得
知识点
分段函数的解析式求法及其图象的作法奇偶函数图象的对称性
1
题型:
单选题
|
8.定义在R上的函数

正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
分段函数的解析式求法及其图象的作法函数的周期性函数的值
1
题型:简答题
|
20.如图,
















(1)求

(2)已知警员的对讲机的有效通话距离是





正确答案
(1)
(2)

解析
(2)甲到达






当

当

所以
因为









知识点
分段函数的解析式求法及其图象的作法余弦定理的应用
1
题型:填空题
|
13.已知函数


正确答案
-4
解析
解析已在路上飞奔,马上就到!
易错点
本题易在理解分段函数性质时发生错误,导致题目无法进行。
知识点
分段函数的解析式求法及其图象的作法函数的最值及其几何意义
下一知识点 : 映射
扫码查看完整答案与解析