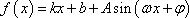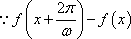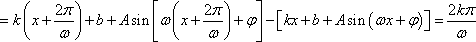- 分段函数的解析式求法及其图象的作法
- 共37题
设










正确答案
解析
略
知识点
若直角坐标平面内的两不同点












正确答案
解析
根据题意可知只须作出函数

知识点
定义:对于函数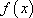
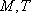
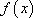

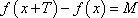
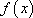
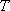
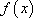
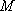
(1)证明函数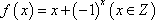
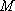
(2)试求一个函数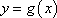
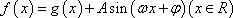
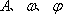
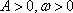
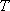
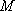
(3)设函数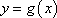
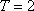
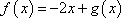
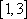
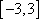
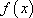
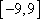
正确答案
见解析
解析
(1)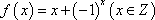
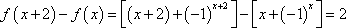
所以函数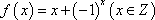
(2)设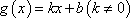
(非零常数) 所以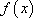
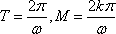
(3)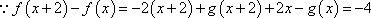
所以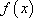
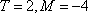
设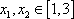
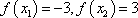
由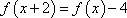
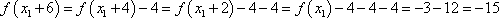
又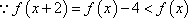
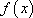
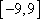

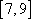
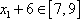
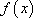
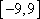
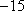
由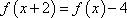
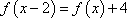
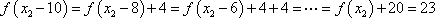
又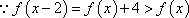
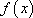
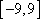

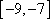
而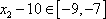
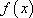
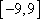
知识点
已知函数f(x)=x﹣[x],其中[x]表示不超过实数x的最大整数,若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是( )
正确答案
解析
函数f(x)=x﹣[x]的图象如下图所示:
y=kx+k表示恒过A(﹣1,0)点斜率为k的直线
若方程f(x)=kx+k有3个相异的实根。
则函数f(x)=x﹣[x]与函数f(x)=kx+k的图象有且仅有3个交点
由图可得:
当y=kx+k过(2,1)点时,k=
当y=kx+k过(3,1)点时,k=
当y=kx+k过(﹣2,﹣1)点时,k=﹣1,
当y=kx+k过(﹣3,﹣1)点时,k=﹣
则实数k满足 


知识点
12.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析