- 多面体和旋转体表面上的最短距离问题
- 共5题
1
题型:填空题
|
棱长为1的正方体



正确答案
解析
知识点
多面体和旋转体表面上的最短距离问题
1
题型:
单选题
|
正确答案
C
解析
依题意,可设

则
又




由①②解得

知识点
多面体和旋转体表面上的最短距离问题
1
题型:
单选题
|
如图,设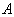
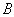
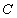
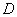
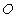
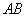
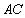
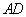
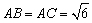
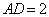
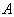
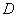
正确答案
C
解析
依题意,可设球的半径为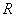
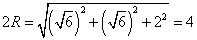
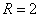
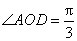
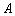
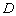
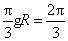
知识点
多面体和旋转体表面上的最短距离问题
1
题型:
单选题
|
某三棱锥的三视图如图所示,该三棱锥的表面积是
正确答案
B
解析
考查的是三棱锥的三视图问题,只不过与往年不同的是这题所求不是棱锥或棱柱的体积而是表面积,因此对于学生计算基本功以及空间想象的双能力都存在着综合性的考查。从所给的三视图可以得到该几何体为三棱锥(已知也已说明),如右图所示。图中蓝色数字所表示的为直接从题目所给三视图中读出的长度,黑色数字代表通过勾股定理的计算得到的边长。本题所求表面积应为三棱锥四个面的面积之和。利用垂直关系和三角形面积公式,可得:10,10,10,
知识点
多面体和旋转体表面上的最短距离问题
1
题型:
单选题
|
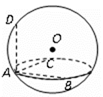
8.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
多面体和旋转体表面上的最短距离问题
下一知识点 : 与球体有关的内切、外接问题
扫码查看完整答案与解析