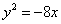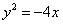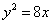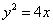- 圆的方程的综合应用
- 共14题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若全集

正确答案
解析



知识点
设单位向量m=(x,y),b=(2,-1),若m⊥b,则|x+2y|=__________.
正确答案
解析
因为m⊥b,所以m·b=2x-y=0.①
又因为m为单位向量,
所以x2+y2=1.②
由①②解得
所以|x+2y|=
知识点
设抛物线的顶点在原点,准线方程为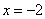
正确答案
解析
选C 由准线方程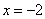
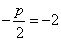
知识点
我区高三期末统一测试中某校的数学成绩分组统计如下表:
(1)求出表中



(2)若我区参加本次考试的学生有

(3)若该校教师拟从分数不超过



正确答案
见解析
解析
(1)解:由频率分布表得
所以


…………5分
(2)由题意知,全区

(3)设考试成绩在


考试成绩在


从不超过

















设抽取的


则事件





知识点
设A是单位圆x2+y2=1上的任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0,且m≠1),当点A在圆上运动时,记点M的轨迹为曲线C。
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标;
(2)过原点且斜率为k的直线交曲线C于P,Q两点,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H.是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由。
正确答案
(1) (0,



解析
(1)如图1,设M(x,y),A(x0,y0),则由|DM|=m|DA|(m>0,且m≠1),可得x=x0,|y|=m|y0|,所以x0=x,|y0|=
因为A点在单位圆上运动,所以x02+y02=1.②
将①式代入②式即得所求曲线C的方程为x2+
因为m∈(0,1)∪(1,+∞),所以
当0<m<1时,曲线C是焦点在x轴上的椭圆,
两焦点坐标分别为(

当m>1时,曲线C是焦点在y轴上的椭圆,
两焦点坐标分别为(0,

(2)方法一:如图2,3,
直线QN的方程为y=2kx+kx1,将其代入椭圆C的方程并整理可得
(m2+4k2)x2+4k2x1x+k2x12-m2=0.
依题意可知此方程的两根为-x1,x2,于是由韦达定理可得
-x1+x2=

因为点H在直线QN上,所以y2-kx1=2kx2=
于是



而PQ⊥PH等价于
即2-m2=0.又m>0,所以
故存在

图1 图2(0<m<1) 图3(m>1)
方法二:如图2,3,
因为P,H两点在椭圆C上,
所以
m2(x12-x22)+(y12-y22)=0.③
依题意,由点P在第一象限可知,点H也在第一象限,且P,H不重合。
故(x1-x2)(x1+x2)≠0,于是由③式可得

又Q,N,H三点共线,所以kQN=kQH,即
于是由④式可得
而PQ⊥PH等价于kPQ·kPH=-1,即
又m>0,得
故存在

知识点
已知集合



正确答案
解析
∵A∪B={1,2}∪{2,3}={1,2,3},U={1,2,3,4},
∴ 
知识点
过点

正确答案
解析
知识点
已知抛物线









(1) 求抛物线
(2)当点


(3)当点


正确答案
(1)
(2)
(3)
解析
(1)依题意




(2)设点


由


∴抛物线



即
∵

∵点


同理, 
综合①、②得,点

∵经过
∴直线


(3)由抛物线的定义可知
所以
联立





知识点
已知a∈R,函数f(x)=4x3-2ax+a。
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0。
正确答案
见解析
解析
(1)解:由题意得f′(x)=12x2-2a。
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞)。
当a>0时,f′(x)=12(x-

此时函数f(x)的单调递增区间为
(-∞,

单调递减区间为[

(2)证明:由于0≤x≤1,故当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2。
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2。
设g(x)=2x3-2x+1,0≤x≤1,
则g′(x)=6x2-2=6(x-

于是
所以,g(x)min=g(

所以当0≤x≤1时,2x3-2x+1>0。
故f(x)+|a-2|≥4x3-4x+2>0。
知识点
扫码查看完整答案与解析