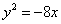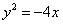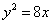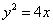· 直线与圆、圆与圆的位置关系

· 圆的方程的综合应用

圆的方程的综合应用
共14题

· 直线与圆、圆与圆的位置关系

· 圆的方程的综合应用

圆的方程的综合应用
共14题

热门试卷

X 查看更多试卷

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：单选题

|

单选题 · 5 分

若全集,则集合等于（）

A

B

C

D

正确答案

D

解析

,,,

知识点

圆的方程的综合应用

1

题型：填空题

|

填空题 · 5 分

设单位向量m＝(x，y)，b＝(2，－1)，若m⊥b，则|x＋2y|＝__________.

正确答案

解析

因为m⊥b，所以m·b＝2x－y＝0.①

又因为m为单位向量，

所以x2＋y2＝1.②

由①②解得或

所以|x＋2y|＝

知识点

圆的方程的综合应用

1

题型：单选题

|

单选题 · 5 分

设抛物线的顶点在原点，准线方程为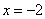，则抛物线的方程是（）

A

B

C

D

正确答案

C

解析

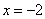
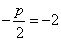
选C 由准线方程得,且抛物线的开口向右（或焦点在轴的正半轴），所以

知识点

圆的方程的综合应用

1

题型：简答题

|

简答题 · 14 分

已知抛物线的顶点为原点，其焦点到直线的距离为，设为直线上的点，过点作抛物线的两条切线，其中为切点。

（1）求抛物线的方程；

（2）当点为直线上的定点时，求直线的方程；

（3）当点在直线上移动时，求的最小值。

正确答案

（1）

（2）

（3）

解析

（1）依题意，解得（负根舍去）

抛物线的方程为；

（2）设点,，，

由,即得.

∴抛物线在点处的切线的方程为，

即.

∵， ∴ 。

∵点在切线上, ∴. ①

同理， . ②

综合①、②得，点的坐标都满足方程 .

∵经过两点的直线是唯一的，

∴直线的方程为，即；

（3）由抛物线的定义可知，

所以

联立，消去得，

当时，取得最小值为

知识点

圆的方程的综合应用

继续学习学习下一知识点

下一知识点 : 与圆有关的最值问题

百度题库 > 高考 > 文科数学 > 圆的方程的综合应用

扫码查看完整答案与解析