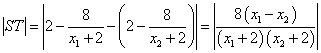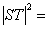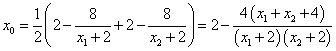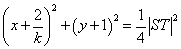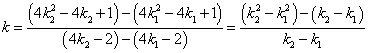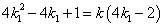- 双曲线的几何性质
- 共220题
1
题型:简答题
|
已知定点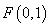
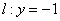

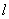
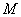
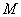
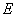
(1) 求曲线
(2) 若点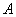

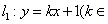
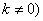
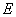
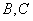
点,直线
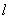
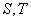
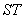
定点? 若是,求这两个定点的坐标;若不是,说明理由。
正确答案
见解析。
解析
(1)解法1:由题意, 点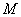
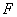

故点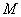

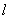
∴曲线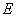
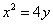
解法2:设点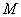
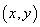
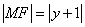
即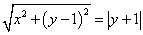
化简得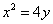
∴曲线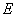
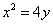
(2) 解法1: 设点
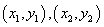
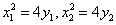
由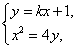
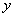
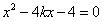
解得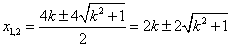
∴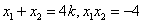
直线
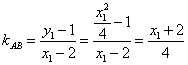
故直线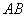
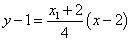
令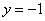
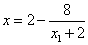
∴点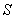
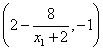
同理可得点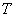
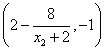
∴
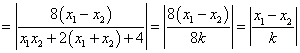
∴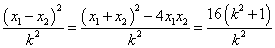
设线段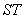
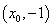
则
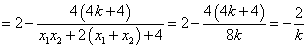
∴以线段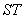
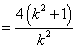
展开得
令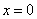
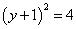
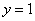
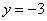
∴以线段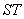
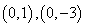
解法2:由(1)得抛物线
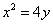
设直线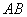
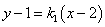
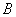
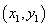
由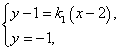
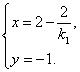
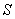
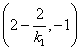
由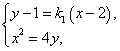
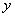
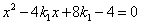
即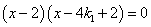
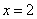
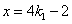
∴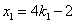
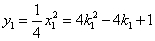
∴点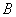
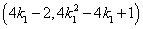
同理,设直线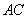
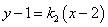
则点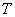
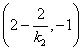
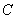
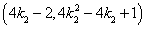
∵点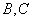
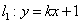
∴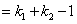
∴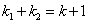
又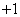
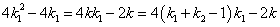
化简得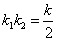
设点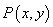
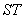
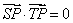
得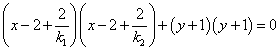
整理得,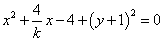
令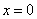
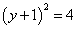
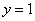
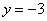
∴以线段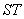
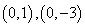
知识点
双曲线的几何性质
1
题型:填空题
|
双曲线
正确答案
解析
略
知识点
双曲线的几何性质
1
题型:
单选题
|
已知函数






正确答案
C
解析
略。
知识点
双曲线的几何性质
1
题型:
单选题
|
双曲线

正确答案
A
解析
略。
知识点
利用基本不等式求最值双曲线的几何性质
1
题型:填空题
|
抛物线



正确答案
解析
略
知识点
双曲线的几何性质
已完结
扫码查看完整答案与解析