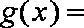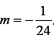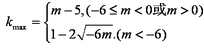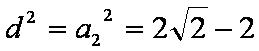- 双曲线的几何性质
- 共220题
设中心在原点的双曲线与椭圆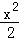
正确答案
2x2﹣2y2=1
解析
解:椭圆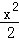
∵中心在原点的双曲线与椭圆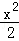
∴双曲线中c=1,
∵椭圆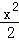
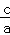
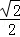
∴双曲线的离心率为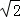
∴双曲线中a=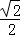
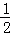
∴双曲线的方程为2x2﹣2y2=1
知识点
过双曲线
正确答案
4x﹣3y﹣20=0
解析
∵双曲线的方程为
∴a2=9,b2=16,得c=
因此,该双曲线右焦点的坐标为F(5,0)
∵双曲线

∴双曲线经过一、三象限的渐近线斜率为k=
∴经过双曲线右焦点,且平行于经过一、三象限的渐近线的直线方程是y=
化为一般式,得4x﹣3y﹣20=0。
故答案为:4x﹣3y﹣20=0
知识点
椭圆
(1)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求推圆方程;
(2)设过F的直线L交椭圆于A,B两点,若直线L绕点F任意转动,恒有

正确答案
(1)
解析
解析:
(2)①当L的斜率不存在时其方程为x=1
从而由

②若L的斜率存在,设其方程为y=k(x-1)
则由


综上得:a的取值范围为
(说明:本题也可由余弦定理及向量知识将⑵转化为
知识点
如图所示, 




(1)求证:

(2)求二面角
正确答案
见解析。
解析
(1)
(2)
由(1)可知,BO⊥平面PAC,故在平面PAC内,作OM⊥A,
连结BM(如图),则∠BMO为二面角
面角,在
即二面角

知识点
已知定义在实数集上的函数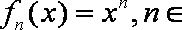

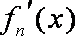
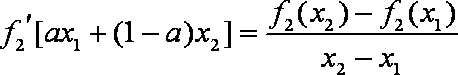
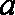
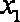
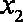

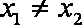
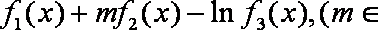
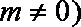
(1)求实数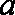
(2)若函数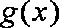
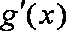
(2)
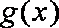
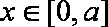

正确答案
(1)
(3)
解析
(1)因为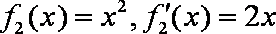
所以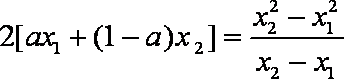
又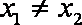
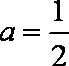
(2)因为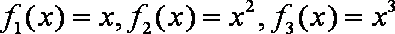
所以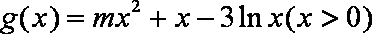
由条件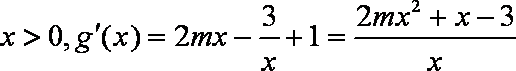
因为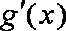
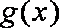
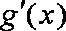
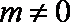
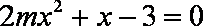

解得
(3)由(1)知,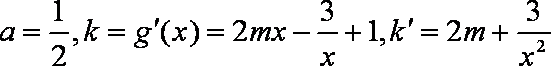
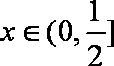
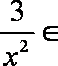
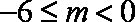
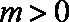
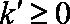
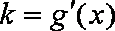

故当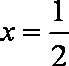

②当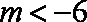
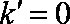
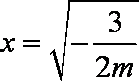
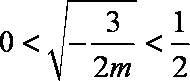
若
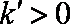
若

故当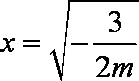
且最大值等于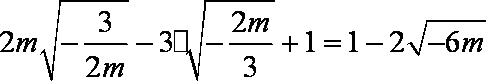
综上,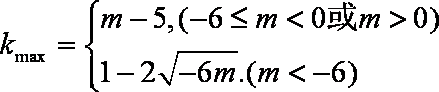
知识点
双曲线










正确答案
解析
由题意可知



知识点
定义:对于两个双曲线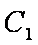
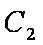
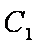
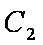
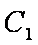
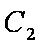
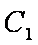
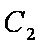
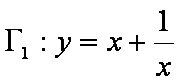
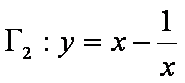
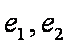
(1)写出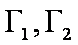
(2)试判断双曲线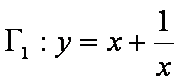
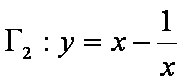
(3)求值: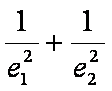
正确答案
见解析。
解析
(1)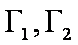
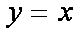
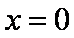
(2)双曲线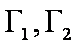
证明如下: 对于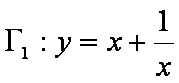
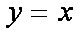
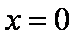
的直线, 所以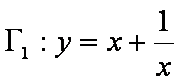
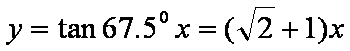
虚轴所在直线为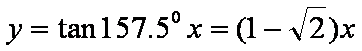
实轴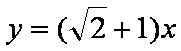

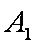
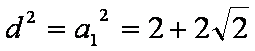
又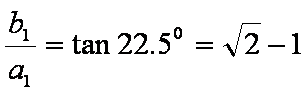
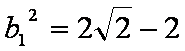
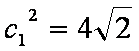
同理对于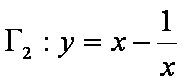
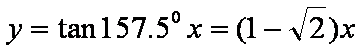
虚轴所在直线为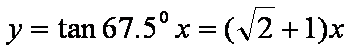
实轴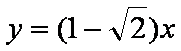

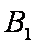
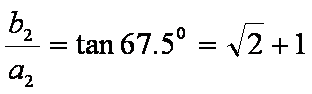
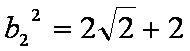

综上所述,双曲线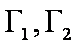
(3) 由(2)易得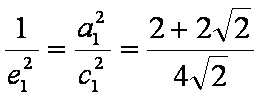
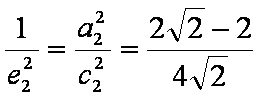
所以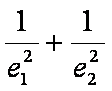
知识点
设






正确答案
解析
由

又


∵



∴
又



知识点








正确答案
解析
略
知识点
离心率为



正确答案
解析
解析:
设椭圆



















知识点
扫码查看完整答案与解析