- 双曲线的几何性质
- 共220题
1
题型:填空题
|
双曲线










正确答案
解析
由题意可知



知识点
等比数列的性质及应用双曲线的几何性质
1
题型:简答题
|
定义:对于两个双曲线
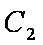
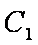
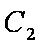
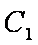
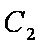
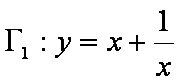
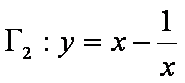
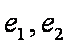
(1)写出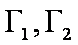
(2)试判断双曲线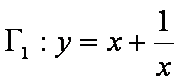
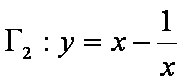
(3)求值: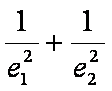
正确答案
见解析。
解析
(1)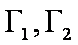
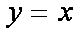
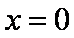
(2)双曲线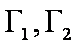
证明如下: 对于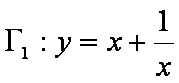
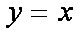
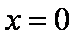
的直线, 所以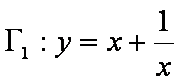
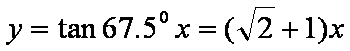
虚轴所在直线为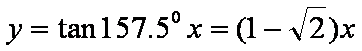
实轴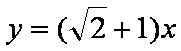

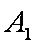
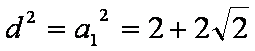
又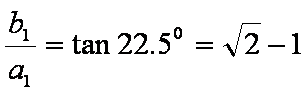
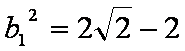
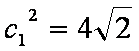
同理对于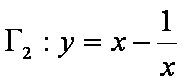
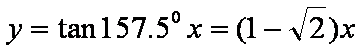
虚轴所在直线为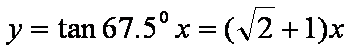
实轴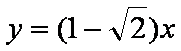

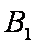
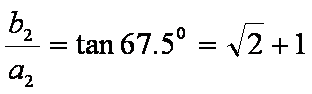
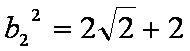

综上所述,双曲线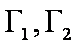
(3) 由(2)易得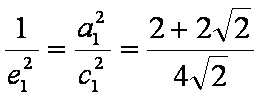
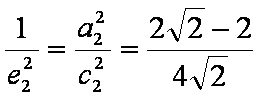
所以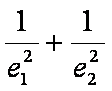
知识点
双曲线的几何性质
1
题型:
单选题
|
设






正确答案
C
解析
由

又


∵



∴
又



知识点
双曲线的几何性质
1
题型:
单选题
|








正确答案
C
解析
略
知识点
向量在几何中的应用双曲线的几何性质
1
题型:
单选题
|
离心率为



正确答案
C
解析
解析:
设椭圆



















知识点
等差数列的性质及应用椭圆的几何性质双曲线的几何性质
已完结
扫码查看完整答案与解析