- 奇偶函数图象的对称性
- 共15题
在平面直角坐标系中,若点














正确答案
1
解析
略
知识点
已知函数
(1)判断
(2)设函数



(3)若

正确答案
见解析
解析
(1)



(2)当



当




当




所以
当




综上,
(3)证法一:
若




令




因为



函数

所以函数

即方程
证法二:
若



即
令



因为


即当

函数
所以函数

所以方程
知识点
9.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若奇函数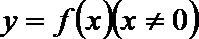
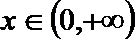
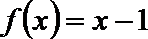
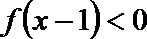
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在实数集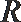
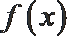
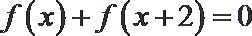
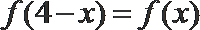
现有以下三种叙述:
①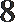
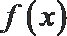
②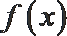
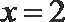
③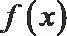
其中正确的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析