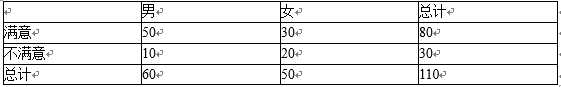- 古典概型的概率
- 共218题
某学校高一、高二、高三年级的学生人数之比为
正确答案
20
解析
略
知识点
通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
(1)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,闷样本中浦意与不满意的女游客各有多少名?
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)很招以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关。
正确答案
见解析。
解析
(1)根据分层抽样可得,样本中满意的女游客有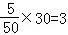
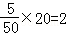
(2)记样本中对景区的服务满意的3名女游客编号为1,2,3,对景区的服务不满意的2名游客编号为4,5,从这5名游客中随机选取两名,共有10个等可能事件为(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)
其中事件A“选到满意与不满意的女游客各一名”包含6个基本事件:(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)
所以所求的概率为P(A)=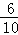
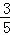
(3)由列联表可得K2=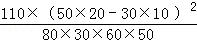
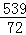
∵P(K2>6.635)=0.010
∴有99%的把握认为“游客性别与对景区的服务满意”有关。
知识点
将容器为n的样本中的数据分成6组,绘制频率分布直方图,若第一组至第六组数据的频率之比为
正确答案
60
解析
知识点
甲、乙两名考生在填报志愿时都选中了



校的面试安排在同一时间.因此甲、乙都只能在这四所院校中选择一所做志愿,假设每位
同学选择各个院校是等可能的,试求:
(1)甲、乙选择同一所院校的概率;
(2)院校

正确答案
见解析
解析
知识点
某人从分别标有1、2、3、4的四张卡片中任意抽取两张,并按如下约定记录抽取结果:如果出现两个偶数或两个奇数,就将两数相加的和记录下来;如果出现一奇一偶,则记下它们的差的绝对值,则出现记录结果不大于3的概率为 .
正确答案
解析
略
知识点
扫码查看完整答案与解析