- 古典概型的概率
- 共218题
18.一个袋中装有四个形状大小完全相同的球,球的编号分别为
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于
(Ⅱ)先从袋中随机取一个




正确答案
(Ⅰ)从袋子中随机取两个球,其一切可能的结果组成的基本事件有:
1和2,1和3,1和4,2和3,2和4,3和4共6个。
从袋中随机取出的求的编号之和不大于4的事件共有1和2,1和3两个。
因此所求事件的概率为
(II)先从袋中随机取一个球,记下编号为m;
放回后,再从袋中随机取一个球,记下编号为n,
其一切可能的结果(m,n)有:
(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4),共16个
有满足条件n≥m+2n的时间的概率为
故满足条件n<m+2的事件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
18.某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从抽取的6名工人中,任取2人,求恰有1名优秀工人的概率.
正确答案
解:
(1)样本均值为
(2)抽取的6名工人中2名为优秀工人,所以12名工人中有4名优秀工人.
(3)抽取的6名工人中2名为优秀工人,设为A,B;4名为非优秀工人,设为a,b,c,d
从A,B,a,b,c,d中任取2人的不同取法有
(A,B),(A,a),(A,b),(A,c),(A,d)
(B,a),(B,b),(B,c),(B,d)
(a,b),(a,c),(a,d)
(b,c),(b,d)
(c,d)共15中,其中恰有1名优秀工人的取法有
(A,a),(A,b),(A,c),(A,d),(B,a),(B,b),(B,c),(B,d)共8种
所以,恰有一名优秀工人的概率是
解析
解析已在路上飞奔,马上就到!
知识点
18.某校从参加高一年级期中考试的学生中随机抽取



观察图形的信息,回答下列问题:
(Ⅰ)求分数在
(Ⅱ)用分层抽样的方法在分数段为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 某品牌汽车
已知分3期付款的频率为0.2,该
(Ⅰ)求上表中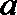
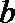
(Ⅱ)该
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为
规定小球掉入
(1)分别求
(2)假设中奖的概率为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.从某学校的










(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的


(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他 们的身高分别为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在1819岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下:(单位:cm)
南方:158,170,166,169,180,175,171,176,162,163;
北方:183,173,169,163,179,171,157,175,178,166;
(1)根据抽测结果,画出茎叶图,并根据你画的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论;
(2)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率。
正确答案
(1)茎叶图如下:
统计结论:(给出下列四个供参考,考生只要答对其中两个即给满分,给出其他合进的答案也给分)
北方大学生的平均身高大于南方大学生的平均身高;
南方大学生的身高比北方大学的身高更整齐;
南方大学生的身高的中位数为169.5cm,北方大学生的身高的中位数为172cm;
南方大学生的高度基本上是对称的,而且大多数集中在均值附近,北方大学生的高度分布较为分散.
(2)南方大学生身高不低于170的有170, 180,175,171,176,从中抽取3个相当于从中抽取2个,共有10种抽法,低于175的只有 2个,所以共有3种,概率为
解析
解析已在路上飞奔,马上就到!
知识点
17.在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩数据统
计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.

(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.
正确答案
解: (1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为
(2)该考场考生“数学与逻辑”科目的平均分为
(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为


设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则
解析
解析已在路上飞奔,马上就到!
知识点
14.从总体数为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的概率为0.25,则N为_________。
正确答案
120
解析
解析已在路上飞奔,马上就到!
知识点
19.为了拓展网络市场,腾讯公司为QQ用户推出了多款QQ应用,如“QQ农场”、“QQ音乐”、“QQ读书”等.市场调查表明,QQ用户在选择以上三种应用时,选择农场、音乐、读书的概率分别为


(1)求三人中恰好有两人选择QQ音乐的概率;
(2)求三人所选择的应用互不相同的概率.
正确答案
解:
(1)三人中恰好有两人选择QQ音乐的概率为P=
(2)记第






他们选择的应用互不相同的概率
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















