- 古典概型的概率
- 共218题
某地区高中分三类,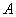
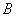
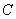
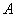
正确答案
200
解析
高中生共有9000人,抽取900,抽取比例为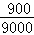
故A类学校中应抽学生
故答案为200。
知识点
某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如下图表所示:
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率。
正确答案
见解析。
解析
(1)由频率表中第1组数据可知,第1组总人数为
再结合频率分布直方图可知
∴a=100×0.020×10×0.9=18,
b=100×0.025×10×0.36=9,

(2)第2,3,4组中回答正确的共有54人。
∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组:
第3组:
第4组:
(3)设第2组的2人为





















其中第2组至少有1人被抽中的有








∴第2组至少有1人获得幸运奖的概率为
知识点
若从总体中随机抽取的样本为
正确答案
解析
略
知识点
对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图。
(1)图中纵坐标

(2)根据图表的数据按分层抽样,抽取

(3)从(2)中抽出的寿命落在



正确答案
见解析。
解析
(1)根据题意:
解得
(2)设在寿命为

解得:
所以应在寿命为

(3)记“恰好有一个寿命为


寿命落在










事件





答:事件“恰好有一个寿命为

知识点
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆。
(1)求z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看作一个总体,从中任取一个分数





正确答案
见解析。
解析
(1)设该厂本月生产轿车为



(2) 8辆轿车的得分的平均数
把8辆轿车的得分看作一个总体,从中任取一个分数

由



知识点
扫码查看完整答案与解析














