- 古典概型的概率
- 共218题
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
①y与x具有正的线性相关关系;
②回归直线过样本点的中心(

③若该大学某女生身高增加1cm,则其体重约增加0.85kg;
④若该大学某女生身高为170cm,则可断定其体重必为58.79kg.
其中正确的结论是 .
正确答案
解析
略
知识点
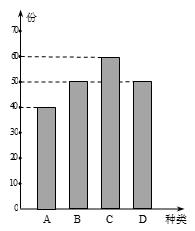
某学校餐厅新推出
(1)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
正确答案
(1)若甲选择的是A款套餐,甲被选中调查的概率是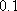
(2)这两人中至少有一人选择的是D款套餐的概率是
解析
(1)由条形图可得,选择A,B,C,D四款套餐的学生共有200人, ……………1分
其中选A款套餐的学生为40人, ……………2分
由分层抽样可得从A款套餐问卷中抽取了 
设事件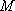
则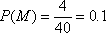
(2)由图表可知,选A,B,C,D四款套餐的学生分别接受调查的人数为4,5,6,5. 其中不满意的人数分别为1,1,0,2个 . ……………7分
记对A款套餐不满意的学生是a;对B款套餐不满意的学生是b;对D款套餐不满意的学生是c,d. ……………8分
设事件N=“从填写不满意的学生中选出2人,至少有一人选择的是D款套餐” …………9分
从填写不满意的学生中选出2人,共有(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)6个基本事件,……10分
而事件N有(a,c),(a,d),(b,c),(b,d),(c,d)5个基本事件, ………11分
则 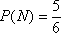
知识点
如果在一次试验中,测得(
根据上表可得回归方程


正确答案
解析
略。
知识点
对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率颁直方图如下:
(1求出表中M,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30]内的概率。
正确答案
见解析。
解析
知识点
已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
见解析。
解析
(1)







(2)由已知:






当


当


当


满足

而基本事件总数为

知识点
扫码查看完整答案与解析